Question

In the adjoining figure, $ABCD$ is a parallelogram. $P$ is a point on $BC$ such that $BP:PC=1:2$. $DP$ produced meets $AB$ produced at $Q$. Given $ar\left( \Delta CPQ \right)=20c{{m}^{2}}$.

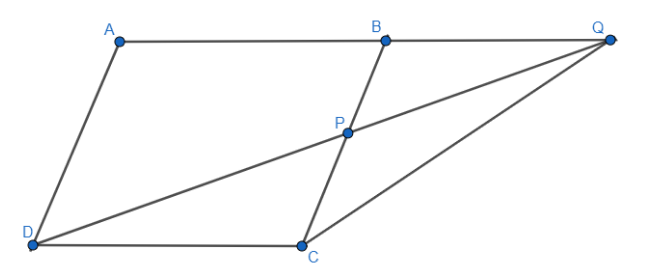
Calculate: (i) $ar\left( \Delta CDP \right)$ (ii) $ar\left( ABCD \right)$

Answer 1

Hint: We start solving this problem by first considering the triangles $BPQ$ and $CPD$ . Then we start proving that those two triangles are similar using the angle-angle similarity. Then we find the area of the $\Delta CDP$ by using the formula $\dfrac{ar\left( \Delta BPQ \right)}{ar\left( \Delta CPD \right)}={{\left( \dfrac{BP}{PC} \right)}^{2}}$ . Then we consider the triangles $BAP$ and $AQD$ as $BP$ is parallel to $AD$ . We again prove that these two triangles are similar using angle-angle similarity. Then we find the area of the triangle $AQD$ by using the formula $\dfrac{ar\left( \Delta AQD \right)}{ar\left( \Delta BQD \right)}={{\left( \dfrac{AQ}{BQ} \right)}^{2}}$ . Then we find the area of the quadrilateral $ADPB$ by subtracting the area of triangle $BPQ$ from the area of triangle $AQD$. Finally, we get the area of the parallelogram $ABCD$ by adding the areas of $\Delta CDP$ and quadrilateral $ADPB$.

Complete step by step answer:
Let us first consider the triangles $BPQ$ and $CPD$.
Now, we get,
$\angle BPQ=\angle CPD$ as they are vertically opposite angles.
$\angle BQP=\angle PDC$ as they are alternate angles.
By angle-angle similarity, we get that $\Delta BPQ$ is similar to $\Delta CPD$
So, we get,
$\dfrac{BP}{CP}=\dfrac{PQ}{PD}=\dfrac{BQ}{CD}$
But we were given that $BP:PC=1:2$ , so,
$\dfrac{BP}{CP}=\dfrac{PQ}{PD}=\dfrac{BQ}{CD}=\dfrac{1}{2}$
Now, let us consider the formula, $\dfrac{ar\left( \Delta BPQ \right)}{ar\left( \Delta CPD \right)}={{\left( \dfrac{BP}{PC} \right)}^{2}}$
By using the above formula, we get,
$\begin{align}
  & \dfrac{ar\left( \Delta BPQ \right)}{ar\left( \Delta CPD \right)}={{\left( \dfrac{1}{2} \right)}^{2}} \\
 & \Rightarrow \dfrac{ar\left( \Delta BPQ \right)}{ar\left( \Delta CPD \right)}=\dfrac{1}{4} \\
\end{align}$
We already know that, $ar\left( \Delta BPQ \right)=\dfrac{1}{2}\times ar\left( \Delta CPQ \right)$
So, we get,
$\begin{align}
  & ar\left( \Delta BPQ \right)=\dfrac{1}{2}\times 20c{{m}^{2}} \\
 & \Rightarrow ar\left( \Delta BPQ \right)=10c{{m}^{2}} \\
\end{align}$
So,
$\begin{align}
  & \dfrac{10}{ar\left( \Delta CPD \right)}=\dfrac{1}{4} \\
 & \Rightarrow ar\left( \Delta CPD \right)=40c{{m}^{2}} \\
\end{align}$
Now, let us consider the triangles $BAP$ and $AQD$.
We get,
$\angle QBP=\angle QAD$ , corresponding angles as $BP$ is parallel to $AD$.
$\angle BQP=\angle AQD$ , as they are common angles.
By Angle-Angle similarity, we get, $\Delta BQP$ is similar to $\Delta AQD$
So, we get, $\dfrac{AQ}{BQ}=\dfrac{QD}{QP}=\dfrac{AD}{BP}$
As, $\dfrac{BP}{CP}=\dfrac{PQ}{PD}=\dfrac{1}{2}$ , we get, $\dfrac{PQ}{QD}=\dfrac{1}{3}$ ,
So, we get, $\dfrac{AQ}{BQ}=\dfrac{QD}{QP}=\dfrac{AD}{BP}=3$ .
Let us consider the formula, $\dfrac{ar\left( \Delta AQD \right)}{ar\left( \Delta BQD \right)}={{\left( \dfrac{AQ}{BQ} \right)}^{2}}$, we get,
$\begin{align}
  & \dfrac{ar\left( \Delta AQD \right)}{ar\left( \Delta BQD \right)}={{\left( \dfrac{AQ}{BQ} \right)}^{2}} \\
 & \Rightarrow \dfrac{ar\left( \Delta AQD \right)}{10}={{\left( 3 \right)}^{2}} \\
 & \Rightarrow \dfrac{ar\left( \Delta AQD \right)}{10}=9 \\
 & \Rightarrow ar\left( \Delta AQD \right)=9\times 10 \\
 & \Rightarrow ar\left( \Delta AQD \right)=90c{{m}^{2}} \\
\end{align}$
Now, let us consider $ar\left( ADPB \right)=ar\left( \Delta AQD \right)-ar\left( \Delta BQP \right)$
We get,
$\begin{align}
  & ar\left( ADPB \right)=ar\left( \Delta AQD \right)-ar\left( \Delta BQP \right) \\
 & \Rightarrow ar\left( ADPB \right)=90-10 \\
 & \Rightarrow ar\left( ADPB \right)=80c{{m}^{2}} \\
\end{align}$
Now, let us consider $ar\left( ABCD \right)=ar\left( \Delta CDP \right)+ar\left( ADPB \right)$
We get,
$\begin{align}
  & ar\left( ABCD \right)=ar\left( \Delta CDP \right)+ar\left( ADPB \right) \\
 & \Rightarrow ar\left( ABCD \right)=40+80 \\
 & \Rightarrow ar\left( ABCD \right)=120c{{m}^{2}} \\
\end{align}$
Hence, we get (i) $ar\left( \Delta CDP \right)=40c{{m}^{2}}$ and (ii) $ar\left( ABCD \right)=120c{{m}^{2}}$

Note:
The possibilities for making mistakes in this type of problem are, one may make a mistake by considering some other inappropriate triangles to get similarity. One must know which triangles are to be taken to check similarity and then proceed to find the required areas.