Question

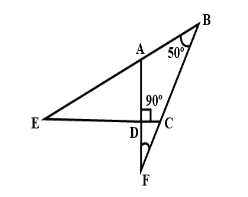
In the adjacent figure, BA and BC are produced to meet CD and AD produced in E and F. Then \[\angle AED + \angle CFD\;\] is ________.

A) \[80^\circ \]
B) \[50^\circ \]
C) \[40^\circ \]
D) \[160^\circ \]

Answer 1

Hint: We will find the angles \[\angle AED\] and \[\angle CFD\] using the properties of triangles like angle sum property and exterior angle property and then add them to get the desired answer.

Complete step-by-step answer:
In \[\Delta AED\],
We will apply angle sum property which states that sum of all angles of a triangle is \[180^\circ \]
Applying angle sum property we get:-
\[\begin{gathered}
  \angle AED + \angle EAD + 90^\circ = 180^\circ \\
   \Rightarrow \angle AED + \angle EAD = 90^\circ \\
   \Rightarrow \angle EAD = 90^\circ - \angle AED...........\left( 1 \right) \\
\end{gathered} \]
In \[\Delta AFB\],
\[\angle EAD\] is the exterior angle
Hence applying exterior angle property which states that the exterior angle is equal to sum of opposite angles.
Therefore,
\[\angle EAD = 50^\circ + \angle AFB............\left( 2 \right)\]
Equating equations 1 and 2 we get:-
\[\begin{gathered}
  50^\circ + \angle AFB = 90^\circ - \angle AED \\
   \Rightarrow \angle AFB + \angle AED = 40^\circ \\
\end{gathered} \]
Now since, \[\angle AFB = \angle CFD\] (corresponding angles)
Therefore, replacing it in above equation we get:-
\[\angle AED + \angle CFD = 40^\circ \]

Hence option (C) is the correct option.

Note: The angle sum property states that sum of all angles of a triangle is \[180^\circ \]
The exterior angle property of a triangle states that the exterior angle is equal to the sum of opposite angles.