Question

In Searle's method to determine the Young’s modulus of a wire, a steel wire of length 156cm and diameter 0.054cm is taken as an experimental wire. The average increase in length for 1.5kgWt is found to be 0.050cm, then the Young’s modulus of the wire is –
\[\begin{align}
  & \text{A) 3}\text{.002}\times \text{1}{{\text{0}}^{11}}N{{m}^{-2}} \\
 & \text{B) 1}\text{.002}\times \text{1}{{\text{0}}^{11}}N{{m}^{-2}} \\
 & \text{C) 2}\text{.002}\times \text{1}{{\text{0}}^{11}}N{{m}^{-2}} \\
 & \text{D) 2}\text{.5}\times \text{1}{{\text{0}}^{11}}N{{m}^{-2}} \\
\end{align}\]

Answer 1

Hint: We can easily find the Young’s modulus by using the relation connecting the length, radius and the elongation of the given experimental wire. All the required quantities are given so we can compute directly the Young’s modulus of the wire.

Complete answer:
We know that Searle's method is one of the most widely used methods to find the Young’s modulus of a given material. It uses two identical wires keeping one as the reference at the same temperature. The Young’s modulus is given by the ratio of the stress applied to the strain as –
\[\text{Young }\!\!'\!\!\text{ s modulus, }Y=\dfrac{Stress}{Strain}\]

                           

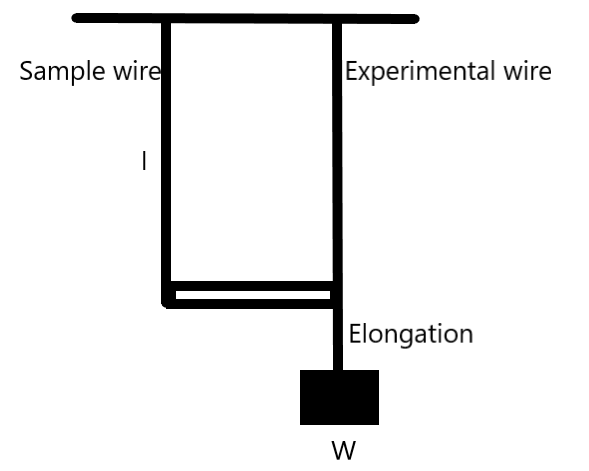
We can substitute the stress and strain in the equation as –
\[\begin{align}
  & Stress=\dfrac{Force}{Area}=\dfrac{mg}{A} \\
 & Strain=\dfrac{\text{Change in length}}{Actual\text{ length}}=\dfrac{\Delta l}{l} \\
 & \Rightarrow Y=\dfrac{mgl}{A\Delta l} \\
\end{align}\]
The area of cross-section of the wire can be computed as –
\[A=\pi {{r}^{2}}\]
Where, r is the radius of the wire.
We can compute the Young’s modulus as –
\[\begin{align}
  & \Rightarrow Y=\dfrac{mgl}{\pi {{r}^{2}}\Delta l} \\
 & \text{given,} \\
 & mg=1.5\times 9.8N=14.7N \\
 & l=156cm=1.56m \\
\end{align}\]
\[\begin{align}
  & r=\dfrac{d}{2}=2.7\times {{10}^{-4}}m \\
 & \Delta l=5\times {{10}^{-4}}m \\
 & \Rightarrow Y=\dfrac{(14.7)(1.56)}{\pi {{(2.7\times {{10}^{-4}})}^{2}}(5\times {{10}^{-4}})} \\
 & \Rightarrow Y=2.002\times {{10}^{11}}N{{m}^{-2}} \\
\end{align}\]
So, the required Young’s modulus of the experimental wire used in the Searle’s method to find the Young’s modulus is given as - \[Y=2.002\times {{10}^{11}}N{{m}^{-2}}\]

So, the correct answer is “Option C”.

Note:
Searle's experiment is used to sample wires hanging side-by-side. This is to cancel any elongations due to temperature during the time of experiment which can affect the value of Young’s modulus drastically. We should take care of it while doing the experiment.