Question

In rectangle $ABCD,{\text{ }}AB = 2l$ and $BC = l.$
Axes $xx’$ and $yy’$ pass through the centre of the rectangle. The moment of inertia is least about

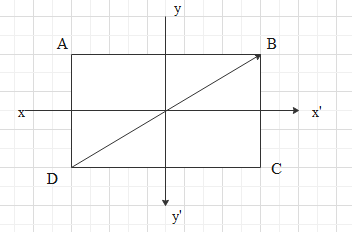
A. DB
B. BC
C. $xx'$
D. $yy'$

Answer 1

Hint: The moment of inertia is dependent on the mass distribution of the body about an axis. Greater the mass and greater the distance of that mass from the axis, larger is the moment of inertia about that axis.

Complete Step-by-Step solution:
Moment of inertia of a body about an axis is defined as the sum of products of masses and distance of masses from the axis.
$$I = \sum\limits_i {{m_i}r_i^2} $$
Where I is the moment of inertia, ${m_i}$ is the ith mass of the body ${r_i}$ is distance of ith mass from the axis of rotation.
Moment of inertia is the resistance faced in rotating a body about an axis. It depends on the mass distribution in the body. Greater the mass and distance of that mass from the axis of rotation, larger is the moment of inertia.
Moment of inertia is minimum about the axis which passes through the centre of mass of the body. For the rectangle ABCD, the centre of mass (COM) is the centre of the rectangle. Therefore, BC is the wrong answer because it doesn’t pass through COM.
Next, we need to check mass distribution about the axes which pass through the COM.
Mass is not uniformly distributed about diagonal BD so this option is also wrong.
Out of xx’ and yy’, we see that in case of xx’ the masses are relatively closer to the axis whereas in case of yy’, the mass is distributed at a larger distance from the axis.
Therefore, the moment of inertia is minimum about the xx' axis because it passes through the COM and mass is uniformly distributed closer to the axis. Hence, the correct answer is option C.

Note: Moment of inertia plays a role only when the body is rotating about an axis. That is why, the axis is always related to the moment of inertia. Moment of inertia is analogous to inertia of the body when it is at rest or in translational motion.