Question

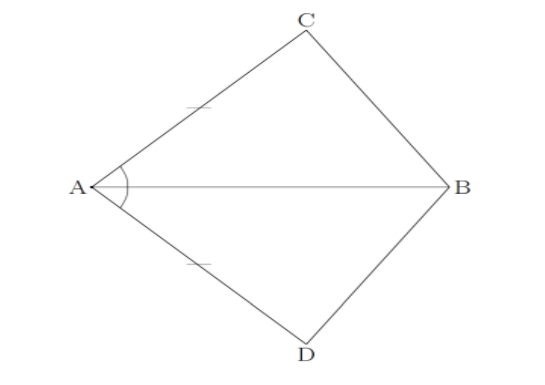
In quadrilateral \[ACBD\],
\[AC = AD\] and \[AB\]bisects \[\left| \!{\underline {\,
  A \,}} \right. \]. Show that \[\Delta \;ABC \cong \Delta \;ABD\]. What can you say about \[BC\]and \[BD\] \[?\]

Answer 1

Hint: First we know, congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal. Here we have to find the pairs of corresponding angles in the given two congruent triangles. We use one of the four rules used to prove whether a given set of triangles are congruent.

Complete step-by-step answer:
They are four rules used to prove whether a given set of triangles are congruent. The four rules are the SSS rule, SAS rule, ASA rule and AAS rule.
Side-Angle-Side (SAS) rule statement: If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent. Side-Side-Side (SSS) rule states that: If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent. Angle-Side-Angle (ASA) rule states that: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent. Angle-Angle-Side (AAS) rule states that: If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
To say the triangles are congruent using the SAS Postulate if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
In \[\Delta ABC\] and \[\Delta ABD\],
Given \[AC = AD\]bisects \[\left| \!{\underline {\,
  A \,}} \right. \]. It means the angle \[\left| \!{\underline {\,
  A \,}} \right. \] divided into two equal angles
i.e., \[\left| \!{\underline {\,
  {CAB} \,}} \right. = \left| \!{\underline {\,
  {DAB} \,}} \right. \]
let \[\left| \!{\underline {\,
  {CAB} \,}} \right. = x = \left| \!{\underline {\,
  {DAB} \,}} \right. \]
Since, the side \[AB\] is same for \[\Delta ABC\]and \[\Delta ABD\]
Hence by SAS congruence rule
\[\Delta ABC \cong \Delta ABD\].
In \[\Delta ABC\],
\[\tan x = \dfrac{{BC}}{{AB}}\]
\[BC = \tan x \times AB\]---(1)
In \[\Delta ABD\],
\[\tan x = \dfrac{{BD}}{{AB}}\]
\[BD = \tan x \times AB\]---(2)
Form the equations (1) and (2), we get
\[BC = BD\]
\[\therefore BC\]and \[BD\] are of equal lengths.

Note: Note that two shapes that are the same size and the same shape are said to be congruent. As long as one of the four rules is true, it is sufficient to prove that the two triangles are congruent. An included angle is an angle formed by two given sides.