
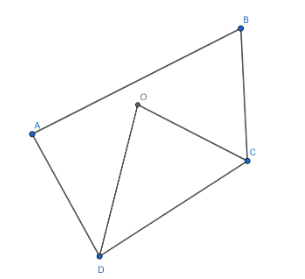
In quadrilateral ABCD, the bisector of angle C and D meet at point O.
Prove that $\angle COD=\dfrac{1}{2}\left( \angle A+\angle B \right)$

Answer
612k+ views
Hint: Use the fact that the sum of angles of a triangle is 180. Hence prove that $\angle COD=180{}^\circ -\dfrac{1}{2}\left( \angle C+\angle D \right)$. Use the angle sum property of a triangle to prove that $\angle C+\angle D=360{}^\circ -\left( \angle A+\angle B \right)$. Substitute the value of $\angle C+\angle D$ in the expression of $\angle COD$ and hence prove the result.
Complete step-by-step answer:
Given: ABCD is a quadrilateral. OD is the angle bisector angle D of the quadrilateral ABCD and OC the angle bisector of angle C of the quadrilateral ABCD.
To prove: $\angle COD=\dfrac{1}{2}\left( \angle A+\angle B \right)$
Proof:
We know that the sum of angles of a triangle is 180(Angle sum property of a triangle).
Hence applying angle sum property in triangle OCD, we get
$\angle COD+\angle DCO+\angle CDO=180{}^\circ \text{ }\left( i \right)$
But since OD is the bisector of angle D of the quadrilateral, we have
$\angle CDO=\dfrac{1}{2}\angle D$
Similarly, since OC is the bisector of angle C of the quadrilateral, we have
$\angle DCO=\dfrac{1}{2}\angle C$
Hence, from equation (i), we have
$\angle COD+\dfrac{1}{2}\angle C+\dfrac{1}{2}\angle D=180{}^\circ $
Taking $\dfrac{1}{2}$ common from the last two terms on LHS, we get
$\angle COD+\dfrac{1}{2}\left( \angle C+\angle D \right)=180{}^\circ $
Also, from the angle sum property of a quadrilateral, we have
$\angle A+\angle B+\angle C+\angle D=360{}^\circ $
Hence, we have
$\angle C+\angle D=360{}^\circ -\left( \angle A+\angle B \right)$
Substituting the value of $\angle C+\angle D$, we get
$\angle COD+\dfrac{1}{2}\left( 360{}^\circ -\left( \angle A+\angle B \right) \right)=180{}^\circ $
Using distributive property, we get
$\angle COD+180{}^\circ -\dfrac{1}{2}\left( \angle A+\angle B \right)=180{}^\circ $
Adding $\dfrac{1}{2}\left( \angle A+\angle B \right)$ on both sides, we get
$\angle COD+180{}^\circ =\dfrac{1}{2}\left( \angle A+\angle B \right)+180{}^\circ $
Subtracting 180 from both sides, we get
$\angle COD=\dfrac{1}{2}\left( \angle A+\angle B \right)$
Note: In these types of questions, we need to remember what the basic properties of quadrilaterals and triangles are and how we can apply them to get the desired result.
Like in the above question, the first focus was to get an equation for COD. Then we followed what changes we could make in RHS so that RHS becomes $\dfrac{\angle A+\angle B}{2}$. This led to the demand of some relation between angles A, B, C and D, which was the angle sum property of the quadrilateral.
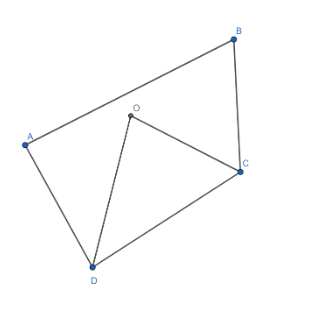
Complete step-by-step answer:

Given: ABCD is a quadrilateral. OD is the angle bisector angle D of the quadrilateral ABCD and OC the angle bisector of angle C of the quadrilateral ABCD.
To prove: $\angle COD=\dfrac{1}{2}\left( \angle A+\angle B \right)$
Proof:
We know that the sum of angles of a triangle is 180(Angle sum property of a triangle).
Hence applying angle sum property in triangle OCD, we get
$\angle COD+\angle DCO+\angle CDO=180{}^\circ \text{ }\left( i \right)$
But since OD is the bisector of angle D of the quadrilateral, we have
$\angle CDO=\dfrac{1}{2}\angle D$
Similarly, since OC is the bisector of angle C of the quadrilateral, we have
$\angle DCO=\dfrac{1}{2}\angle C$
Hence, from equation (i), we have
$\angle COD+\dfrac{1}{2}\angle C+\dfrac{1}{2}\angle D=180{}^\circ $
Taking $\dfrac{1}{2}$ common from the last two terms on LHS, we get
$\angle COD+\dfrac{1}{2}\left( \angle C+\angle D \right)=180{}^\circ $
Also, from the angle sum property of a quadrilateral, we have
$\angle A+\angle B+\angle C+\angle D=360{}^\circ $
Hence, we have
$\angle C+\angle D=360{}^\circ -\left( \angle A+\angle B \right)$
Substituting the value of $\angle C+\angle D$, we get
$\angle COD+\dfrac{1}{2}\left( 360{}^\circ -\left( \angle A+\angle B \right) \right)=180{}^\circ $
Using distributive property, we get
$\angle COD+180{}^\circ -\dfrac{1}{2}\left( \angle A+\angle B \right)=180{}^\circ $
Adding $\dfrac{1}{2}\left( \angle A+\angle B \right)$ on both sides, we get
$\angle COD+180{}^\circ =\dfrac{1}{2}\left( \angle A+\angle B \right)+180{}^\circ $
Subtracting 180 from both sides, we get
$\angle COD=\dfrac{1}{2}\left( \angle A+\angle B \right)$
Note: In these types of questions, we need to remember what the basic properties of quadrilaterals and triangles are and how we can apply them to get the desired result.
Like in the above question, the first focus was to get an equation for COD. Then we followed what changes we could make in RHS so that RHS becomes $\dfrac{\angle A+\angle B}{2}$. This led to the demand of some relation between angles A, B, C and D, which was the angle sum property of the quadrilateral.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?

Draw the diagram of the sectional view of the human class 10 biology CBSE




