
In quadrilateral $ ABCD $ , diagonals $ AC $ and $ BD $ intersect at point $ E $ such that $ AE:EC = BE:ED $ .
Show that: $ ABCD $ is a trapezium.
Answer
564.6k+ views
Hint: In this question, we need to prove $ ABCD $ is a trapezium. Here, we will construct a quadrilateral $ ABCD $ with diagonals $ AC $ and $ BD $ intersect at point $ E $ . Then, using the properties of basic proportionality theorem, vertically opposite angles, SAS similarity theorem, corresponding angles congruence we will determine $ ABCD $ is a trapezium.
Complete step-by-step answer:
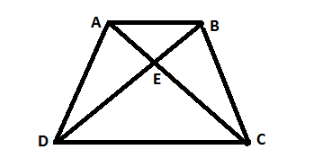
Now, we have constructed a quadrilateral $ ABCD $ with diagonals $ AC $ and $ BD $ intersect at point $ E $ .
Then, $ \dfrac{{AE}}{{EC}} = \dfrac{{BE}}{{ED}} $
$ \dfrac{{AE}}{{BE}} = \dfrac{{EC}}{{ED}} $
Let this be equation (1),
In $ \Delta ABE $ and $ \Delta CDE $ ,
Therefore, from equation (1),
$ \dfrac{{AE}}{{BE}} = \dfrac{{EC}}{{ED}} $
We know that vertically opposite angles are equal. Therefore, we have,
$ \angle ABE = \angle DEC $
Then, we also know that, the SAS similarity theorem states that if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
Therefore, by the theorem, we have,
$ \Delta ABE \sim \Delta CDE $
Here, the corresponding angles are equal,
$ \angle EDC = \angle EBA $
Therefore,
$ \angle BDC = \angle ABD $
From the figure we can say this is a pair of alternate angles.
Thus, $ AB\parallel DC $
Hence, the quadrilateral $ ABCD $ is trapezium.
So, the correct answer is “ $ ABCD $ is trapezium”.
Note: It is important to note here that vertically opposite angles are the angles opposite to each other when two lines cross. These angles are equal. Also, the angle rule of corresponding angles states that the corresponding angles are equal if a transversal cuts two parallel lines. However, we can also prove this by constructing a line $ EF $ where $ F $ in the side $ AD $ . Then, we can use basic proportionality theorem and converse of basic proportionality theorem to prove $ ABCD $ is a trapezium.
Complete step-by-step answer:

Now, we have constructed a quadrilateral $ ABCD $ with diagonals $ AC $ and $ BD $ intersect at point $ E $ .
Then, $ \dfrac{{AE}}{{EC}} = \dfrac{{BE}}{{ED}} $
$ \dfrac{{AE}}{{BE}} = \dfrac{{EC}}{{ED}} $
Let this be equation (1),
In $ \Delta ABE $ and $ \Delta CDE $ ,
Therefore, from equation (1),
$ \dfrac{{AE}}{{BE}} = \dfrac{{EC}}{{ED}} $
We know that vertically opposite angles are equal. Therefore, we have,
$ \angle ABE = \angle DEC $
Then, we also know that, the SAS similarity theorem states that if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
Therefore, by the theorem, we have,
$ \Delta ABE \sim \Delta CDE $
Here, the corresponding angles are equal,
$ \angle EDC = \angle EBA $
Therefore,
$ \angle BDC = \angle ABD $
From the figure we can say this is a pair of alternate angles.
Thus, $ AB\parallel DC $
Hence, the quadrilateral $ ABCD $ is trapezium.
So, the correct answer is “ $ ABCD $ is trapezium”.
Note: It is important to note here that vertically opposite angles are the angles opposite to each other when two lines cross. These angles are equal. Also, the angle rule of corresponding angles states that the corresponding angles are equal if a transversal cuts two parallel lines. However, we can also prove this by constructing a line $ EF $ where $ F $ in the side $ AD $ . Then, we can use basic proportionality theorem and converse of basic proportionality theorem to prove $ ABCD $ is a trapezium.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What are the 12 elements of nature class 8 chemistry CBSE

What is the difference between rai and mustard see class 8 biology CBSE

When people say No pun intended what does that mea class 8 english CBSE

Write a short biography of Dr APJ Abdul Kalam under class 8 english CBSE

Write a letter to the Municipal Commissioner to inform class 8 english CBSE

Compare the manure and fertilizer in maintaining the class 8 biology CBSE




