Question

In quadrilateral $ABCD$, $CO$ and $DO$ are the bisectors of $\angle C$ and $\angle D$ respectively. Prove that $\angle COD = \dfrac{1}{2}(\angle A + \angle B)$.

Answer 1

Hint: We will use two theorems to solve this problem. First is the sum of all interior angles of a triangle is ${180^ \circ }$ and the other is the sum of all interior angles of a quadrilateral is ${360^ \circ }$. We will draw the diagram of the quadrilateral for a better understanding.

Complete step-by-step solution:
First, we will draw the figure of quadrilateral $ABCD$ with bisectors $CO$ and $DO$ respectively.

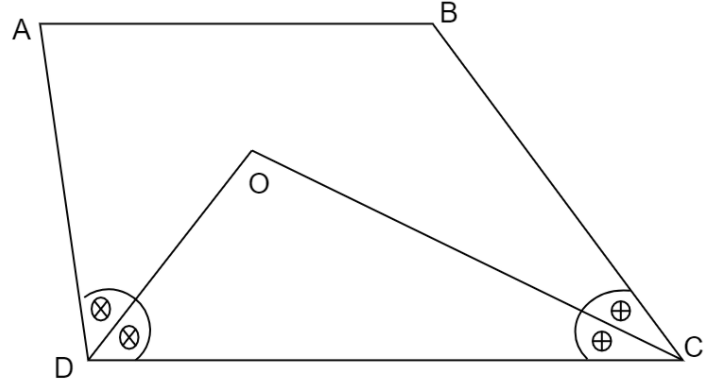
Consider $\square ABCD$,
In $\square ABCD$,$CO$ and $DO$ are the bisectors of $\angle C$ and $\angle D$ respectively.
Therefore, we get,
$\angle OCD = \dfrac{1}{2}\angle C$ and $\angle ODC = \dfrac{1}{2}\angle D$ …. (1)
Applying the theorem: The sum of all interior angles of a quadrilateral is ${360^ \circ }$.
$\angle A + \angle B + \angle C + \angle D = {360^ \circ }$
Rearranging the terms,
$\angle C + \angle D = {360^ \circ } - \left( {\angle A + \angle B} \right)$ ….. (2)
Consider $\Delta COD$,
Applying the theorem: the sum of all interior angles of a triangle is ${180^ \circ }$.
We get,
$\angle COD + \angle OCD + \angle ODC = {180^ \circ }$
Rearranging the terms,
$\angle COD = {180^ \circ } - \left( {\angle OCD + \angle ODC} \right)$
From equation (1), we can substitute the values of angles as,
$\angle COD = {180^ \circ } - \left( {\dfrac{1}{2}\angle C + \dfrac{1}{2}\angle D} \right)$
Taking $\dfrac{1}{2}$ common we get,
$\angle COD = {180^ \circ } - \dfrac{1}{2}\left( {\angle C + \angle D} \right)$
From equation (2), substituting the values,
$\angle COD = {180^ \circ } - \dfrac{1}{2}\left( {{{360}^ \circ } - \left( {\angle A + \angle B} \right)} \right)$
Multiplying the $\dfrac{1}{2}$ term with the bracket term,
$\angle COD = {180^ \circ } - \left( {\dfrac{1}{2} \times {{360}^ \circ } - \dfrac{1}{2}\left( {\angle A + \angle B} \right)} \right)$
Canceling the terms,
$\angle COD = {180^ \circ } - {180^ \circ } + \dfrac{1}{2}\left( {\angle A + \angle B} \right)$
Subtracting the terms,
$\angle COD = \dfrac{1}{2}\left( {\angle A + \angle B} \right)$
Hence proved.

Note: Angle bisectors divide the angle into two equal half angles. The sum of all interior angles of a quadrilateral is ${360^ \circ }$ and the sum of all interior angles of a triangle is ${180^ \circ }$ is called the angle sum property of a quadrilateral and triangle respectively. Every angle inside a triangle is less than ${180^ \circ }$ and every angle inside a quadrilateral is also less than ${180^ \circ }$ .