Question

In Pythagoras theorem in right angled triangle the longest side is called the
A) Hypotenuse
B) Height
C) Perpendicular
D) Bisector

Answer 1

Hint:
Here, we will first draw the right-angled triangle and state its different sides. Then we will state Pythagoras theorem and find out what is the longest side of the right-angled triangle called.

Complete step by step solution:
First, we will draw the right-angled triangle here. A right-angled triangle is a triangle in which one angle is \[90^\circ \] and also the sum of the other two angles of a right-angled triangle is \[90^\circ \].

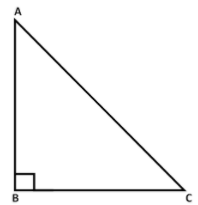
The right-angle triangle consists of three sides named as perpendicular, base and hypotenuse. We also have a relation between base, perpendicular, and hypotenuse of a right-angle triangle from Pythagoras theorem. Pythagoras theorem states that the square of the hypotenuse is equal to the sum of squares of base and perpendicular sides of a right angles triangle.
Thus, the longest side of a right-angled triangle is called a hypotenuse.
Here, in \[\Delta ABC\], \[AC\] is the hypotenuse and it is just opposite to the right angle i.e. \[\angle ABC\] of \[\Delta ABC\].
Using Pythagoras theorem in \[\Delta ABC\], we get
\[A{C^2} = A{B^2} + B{C^2}\]
AC is the longest side of the right-angled triangle and it is called the hypotenuse.

Thus, the correct option is option A.

Note:
Pythagoras theorem can only be used in the right-angled triangle and not in any other triangle. We need to keep in mind that the sum of any two sides of a triangle is always greater than the third side. In a right-angle triangle also, the sum of the length of the base and perpendicular is greater than the hypotenuse.