Question

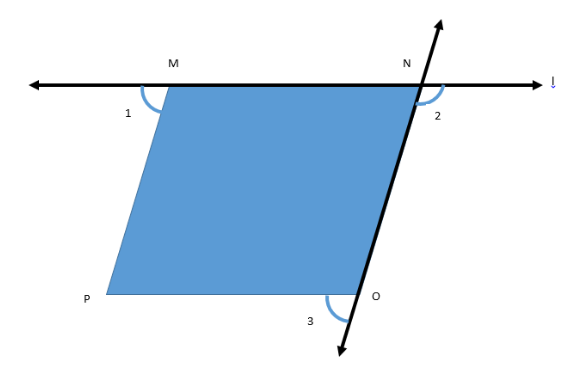
In parallelogram MNOP, MN is a part of line l. Find the measure of the :
1) $\angle 1 + \angle 2$
2) $\angle 2 + \angle 3$

Answer 1

Hint: We will use the fact that opposite sides of a parallelogram are parallel and then treating NO as a transverse, we will use the alternate angles’ theory for 2 and 3 angles. Now, we will use the fact that adjacent angles of a parallelogram are supplementary.

Complete step-by-step answer:
Part 1)
We know that the adjacent angles of a parallelogram are supplementary.
Therefore, we will have that: $\angle PMN + \angle MNO = {180^ \circ }$ ………..(1)
Now, since l is a straight line and MN is a part of it.
Hence, $\angle PMN + \angle 1$ and $\angle MNO + \angle 2$ are the linear pairs.
Hence, $\angle PMN + \angle 1 = {180^ \circ }$ ………(2)
and $\angle MNO + \angle 2 = {180^ \circ }$ ……………(3)
Now, adding (2) and (3), we will get:-
$ \Rightarrow \angle PMN + \angle 1 + \angle MNO + \angle 2 = {360^ \circ }$
We can rewrite it as:-
$ \Rightarrow \angle PMN + \angle MNO + \angle 1 + \angle 2 = {360^ \circ }$
Using (1) in this, we will get:-
$ \Rightarrow {180^ \circ } + \angle 1 + \angle 2 = {360^ \circ }$
Taking ${180^ \circ }$ from the LHS to RHS, we will get:-
$ \Rightarrow \angle 1 + \angle 2 = {360^ \circ } - {180^ \circ }$
On simplifying the RHS, we will get:-
$ \Rightarrow \angle 1 + \angle 2 = {180^ \circ }$
Part 2)
We know that the opposite lines of a parallelogram are always parallel.
Hence, MN will be parallel to OP and NO will be parallel to OP.
Now, since MN and OP are parallel to each other and the line NO is acting as a transversal between them.
Hence, $\angle 2 = \angle NOP$ (Because of Alternate angles) …………..(4)
[Alternate angles are angles that are in opposite positions relative to a transversal intersecting two lines]
$\angle NOP + \angle 3$ and $\angle MNO + \angle 2$ are the linear pairs.
Hence, $\angle NOP + \angle 3 = {180^ \circ }$ ………(5)
Using (4) in this, we will get:-
$\angle 2 + \angle 3 = {180^ \circ }$.

Note: The students must note that if they are given to find some relation between angles 1 and 3, they can do so as well. Remember that the opposite angles of a parallelogram are equal and angle 1 and angle 3 are just the supplementary of equal angles and hence, must be equal as well.
Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees (straight line) . One of the supplementary angles is said to be the supplement of the other. The two angles do not need to be together or adjacent. They just need to add up to 180 degrees. If the two supplementary angles are adjacent then they will form a straight line.