Question

In parallelogram \[MNOP\], \[MN\] is a part of Line \[L\].

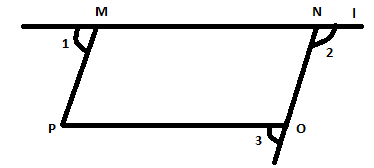
A) Find the measure of \[\angle 1 + \angle 2\].
B) Find the measure of \[\angle 2 + \angle 3\] .

Answer 1

Hint: In this question, we have to find the measure of addition of angles. We are going to solve this problem by using some geometrical properties.
If two parallel lines are intersected by one line the corresponding angles are equal.
If we consider the angle over a straight line it is \[180^\circ \].
Thus we can use these two ideas to solve the given problem.

Complete step-by-step answer:
It is given that, in the given parallelogram \[MNOP\], \[MN\] is a part of Line $L$.

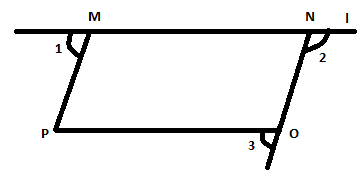
We need to find out the measure of \[\angle 1 + \angle 2\] &\[\angle 2 + \angle 3\].
We know, in a parallelogram opposite sides are parallel.
So we get, \[MP\parallel NO\] and \[MN\parallel PO\].
A) Thus, \[MP\parallel NO\] and \[L\] is the intersecting line.
We know, when the two lines being crossed by one line are Parallel Lines the Corresponding Angles are equal.
Thus \[\angle 1 = \angle MNO\]
Again, since the angle over a straight line is \[180^\circ \], \[\angle MNO + \angle 2 = 180^\circ \]
Therefore, \[\angle 1 + \angle 2 = 180^\circ \][using, \[\angle 1 = \angle MNO\]]
B) We have, \[MN\parallel PO\] and \[NO\] is the intersecting line.
We know, when the two lines being crossed by one line are Parallel Lines the Corresponding Angles are equal.
Thus \[\angle 3 = \angle MNO\]
Again, since the angle over a straight line is \[180^\circ \], \[\angle MNO + \angle 2 = 180^\circ \]
Therefore, \[\angle 3 + \angle 2 = 180^\circ \] [using, \[\angle 3 = \angle MNO\]]

Hence, the measure of \[\angle 1 + \angle 2\] is \[180^\circ \]
The measure of \[\angle 2 + \angle 3\] is \[180^\circ \].

Note: Here we are finding the measure of two angles by doing addition. So we must use the diagram for our understanding. We have made it clear and simple with the given attributes.
Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line.

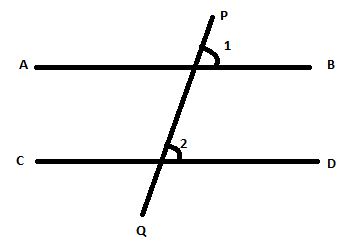
Here \[\angle 1\& \angle 2\] are corresponding angles.
When the two lines being crossed by one line are Parallel Lines the Corresponding Angles are equal.
Thus, here \[\angle 1 = \angle 2\]