Question

In Parallelogram $ABCD$, the bisectors of the consecutive angles $\angle A$ and $\angle B$ intersect at $P$ then prove that $\angle APB = {90^0}$.

Answer 1

Hint: We have been given that $ABCD$ is a parallelogram. So opposite sides will be parallel to each other and the sum of adjacent angles will be equal to \[{180^0}\]. So half of the sum of the adjacent angle will be equal to \[{90^0}\]. After that we take triangle $ABP$ and apply angle sum properly. Then we put the value of angles from the above known value and this will help us to prove the result.

Complete step-by-step answer:
We have given that $ABCD$ is a parallelogram and angle bisector of angle $A$ and angle $B$ meets at $P$.
We have to prove $\angle APB = {90^0}$
Now $AD\parallel BC$ and $AB\parallel DC$
$AB$ acts as the transversal for $AD$ and $BC$.

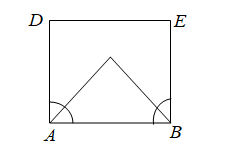
We know that sum of interior angles of a transverse of is equal to \[{180^0}\]
So $\angle DAB + \angle CBA = {180^0}$ ------(i)
Now $AP$ and $BP$ are the transversal of the $\angle DAB$ and $\angle CBA$ respectively.
So $\dfrac{1}{2}\angle DAB = \angle PAB$ and $\dfrac{1}{2}\angle CBA = \angle PBA$
Putting these values in equation (i)
$2\angle PAB + 2\angle PBA = {180^0}$
$\angle PAB + \angle PBA = \dfrac{{180}}{2} = {90^0}$
$\angle PAB + \angle PBA = {90^0}$ --------(ii)
$P$ is the interesting point of $AP$ and $BP$. So $ABP$ is a triangle.
Sum of internal angle of triangle = ${180^0}$ .
Therefore $\angle PAB + \angle PBA + \angle ABP = {180^0}$
${90^0} + \angle ABP = {180^0}$
$\angle ABP = {180^0} - {90^0}$
$\angle ABP = {90^0}$

Hence we have proved.

Note: In Euclidean geometry, parallelogram is simple quadrilaterals, which have two parts of parallel sides. The opposite sides of the parallelogram are of equal length and the opposite angles of parallelogram are of equal measure.
There are some properties of parallelograms.
The consecutive angles of the parallelograms are supplementary. This means the sum of consecutive angles of the parallelogram is equal to \[{180^0}\] .
Diagonal of the parallelograms bisects each other.
Each diagonal of the parallelograms separates it into two congruent triangles.