
In parallelogram ABCD, E and F are mid points of the sides AB and CD respectively. The line segment AF and BF meet the line segment ED and EC at point G and H respectively. Prove that:
(i) Triangle HEB and FHC are congruent
(ii) GEHF is a parallelogram.
Answer
559.8k+ views
Hint:
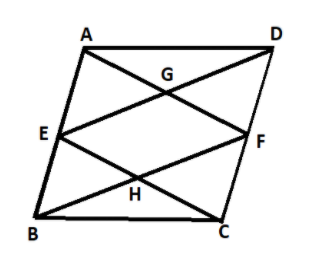
Draw the diagram first. Given that, in parallelogram ABCD, E and F are mid points of the sides AB and CD respectively; i.e. AE = BE = CF = DF (since AB = CD). Now we can easily show $\vartriangle BEH\; \cong \vartriangle FHC$ by AAS rule of congruence.
For the second proof, note that the quadrilateral AECF and BEDF are both parallelograms, since one pair of their sides are equal and parallel. Therefore, $EH\parallel GF$ and $EG\parallel HF$. So both of the pairs of sides of the quadrilateral GEHF are parallel. Therefore quadrilateral GEHF is a parallelogram.
Complete step-by-step answer:
In parallelogram ABCD, E and F are mid points of the sides AB and CD respectively.
$\Rightarrow$ AE = BE and CF = DF
$\Rightarrow$ AE = BE = CF = DF … (since AB = CD)
Given that, the line segments AF and BF meet the line segments ED and EC at point G and H respectively.
Now, in $\vartriangle BEH$ and $\vartriangle FHC$,
BE = CF
$\angle BEH = \angle CHF$ (vertically opposite angles)
$\angle BEH = \angle HCF$ (alternate angles; since $AB\parallel CD$, EC transversal)
Therefore, $\vartriangle BEH\; \cong \vartriangle FHC$ (by AAS rule of congruence)
Proved (i)
Again, note that the quadrilateral AECF is a parallelogram, since one pair of its sides are equal and parallel.
$\Rightarrow$ $EC\parallel AF$
$\Rightarrow$ $EH\parallel GF$
Similarly, quadrilateral BEDF is also a parallelogram.
$\Rightarrow$ $ED\parallel BF$
$\Rightarrow$ $EG\parallel HF$
So both of the pairs of opposite sides of the quadrilateral GEHF are parallel.
Therefore, quadrilateral GEHF is a parallelogram.
Note:
The four rules of congruency are as follows:
SSS: When three sides of two different triangles are equal in length.
SAS: When two sides are equal, and the angle between them is also the same in measure.
AAS: When any two angles and a side is equal.
RHS: When the hypotenuse and any one side of two right angled triangles are equal in length.
Also, note the following properties of a parallelogram.
Both the pairs of opposite sides are equal and parallel to each other.
Both the pairs of opposite angles are equal.
Any two consecutive angles (or same-side interior angles) are supplementary.
The diagonals are equal in length.
The diagonals intersect each other.
The diagonal divides the parallelogram in two congruent triangles.

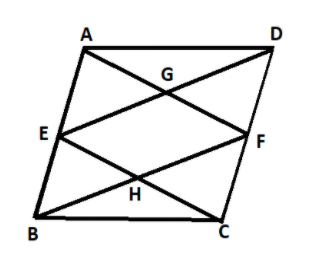
Draw the diagram first. Given that, in parallelogram ABCD, E and F are mid points of the sides AB and CD respectively; i.e. AE = BE = CF = DF (since AB = CD). Now we can easily show $\vartriangle BEH\; \cong \vartriangle FHC$ by AAS rule of congruence.
For the second proof, note that the quadrilateral AECF and BEDF are both parallelograms, since one pair of their sides are equal and parallel. Therefore, $EH\parallel GF$ and $EG\parallel HF$. So both of the pairs of sides of the quadrilateral GEHF are parallel. Therefore quadrilateral GEHF is a parallelogram.
Complete step-by-step answer:

In parallelogram ABCD, E and F are mid points of the sides AB and CD respectively.
$\Rightarrow$ AE = BE and CF = DF
$\Rightarrow$ AE = BE = CF = DF … (since AB = CD)
Given that, the line segments AF and BF meet the line segments ED and EC at point G and H respectively.
Now, in $\vartriangle BEH$ and $\vartriangle FHC$,
BE = CF
$\angle BEH = \angle CHF$ (vertically opposite angles)
$\angle BEH = \angle HCF$ (alternate angles; since $AB\parallel CD$, EC transversal)
Therefore, $\vartriangle BEH\; \cong \vartriangle FHC$ (by AAS rule of congruence)
Proved (i)
Again, note that the quadrilateral AECF is a parallelogram, since one pair of its sides are equal and parallel.
$\Rightarrow$ $EC\parallel AF$
$\Rightarrow$ $EH\parallel GF$
Similarly, quadrilateral BEDF is also a parallelogram.
$\Rightarrow$ $ED\parallel BF$
$\Rightarrow$ $EG\parallel HF$
So both of the pairs of opposite sides of the quadrilateral GEHF are parallel.
Therefore, quadrilateral GEHF is a parallelogram.
Note:
The four rules of congruency are as follows:
SSS: When three sides of two different triangles are equal in length.
SAS: When two sides are equal, and the angle between them is also the same in measure.
AAS: When any two angles and a side is equal.
RHS: When the hypotenuse and any one side of two right angled triangles are equal in length.
Also, note the following properties of a parallelogram.
Both the pairs of opposite sides are equal and parallel to each other.
Both the pairs of opposite angles are equal.
Any two consecutive angles (or same-side interior angles) are supplementary.
The diagonals are equal in length.
The diagonals intersect each other.
The diagonal divides the parallelogram in two congruent triangles.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




