Question

In maximization problem, optimal solution occurring at corner point yields the-
A. mean values of z
B. highest value of z
C. lowest value of z
D. mid value of z

Answer 1

Hint: The basic concepts of linear programming will be applied here. Linear programming or mathematical modeling is a technique in which a linear function is maximized or minimized when subjected to various constraints. Here, we will identify which type of problem is under consideration, and check the options for what will the corner point yield.

Complete step-by-step answer:

We need to find what is the optimal solution occurring at a corner point yields a maximization problem. There is a particular method to solve LPP problems. All the equations and constraints are plotted on a graph, and all the corner points are checked, which gives an optimum maximum or minimum condition for a function. For example-
Maximize $z:3x + 4y$ subject to constraints $x + y \leqslant 4,\;x \geqslant 0,\;y \geqslant 0$

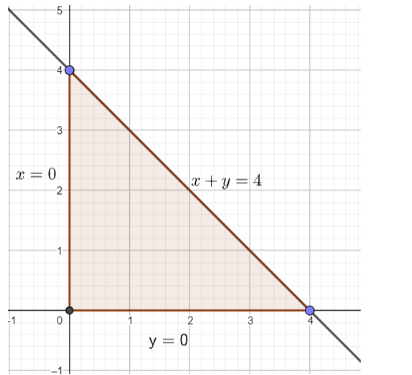
We can see that the corner points of the triangle formed are (0, 0), (4, 0) and (0, 4). We will substitute these values of x and y in z, to get the maxima.

This implies that the optimal solution occurring at the corner points gives the highest value of z. So the correct option is B.

Note: In reality, we can get both the maxima and minima from the corner points, under a given set of constraints. So students might get confused which option is right. But when we look closely, it is specifically mentioned that we need to consider a maximization problem, so we need to find the highest value of z, which clears the confusion.