Question

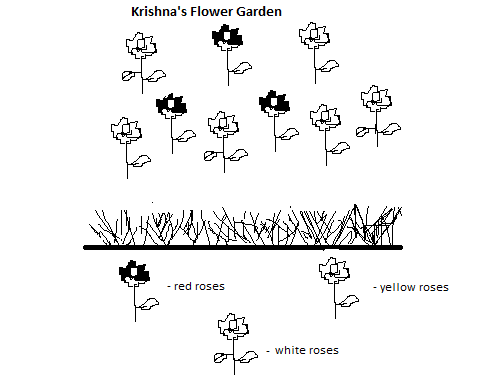
In Krishna’s flower garden, $\dfrac{1}{7}$are white roses,$\dfrac{4}{7}$are yellow roses and the rest are red roses.

A. $\dfrac{1}{7}$
B. $\dfrac{2}{7}$
C. $\dfrac{3}{7}$
D. $\dfrac{4}{7}$

Answer 1

Hint: From the above question we can see that there are red roses, yellow roses and white roses. We were given the ratios of white roses and yellow roses from the garden. In order to find the red roses we will add all the ratios (fractions) and equal it to 1 (garden). This will look like$\dfrac{1}{7}$+$\dfrac{4}{7}$+ x = 1 (say red roses be x). On solving this equation we will get the ratio of red roses.

Complete step by step answer:
Given:
A garden consists of white roses, yellow roses and red roses.
Number of white roses =$\dfrac{1}{7}$
Number of yellow roses=$\dfrac{4}{7}$
Let the total number of roses in the garden be 1.
Rest of the roses are red and let it be x.
Ratio: A ratio is a comparison of two or more numbers that indicates their sizes in relation to each other. A ratio compares two quantities by division, with the dividend or number being divided termed the antecedent and the divisor or number that is dividing termed as consequent.
A part to whole comparison measures the number of one against the total.
$ \Rightarrow $$\dfrac{1}{7}$+$\dfrac{4}{7}$+ x = 1
$ \Rightarrow \dfrac{{1 + 4 + 7x}}{7} = 1$
$ \Rightarrow \dfrac{{5 + 7x}}{7} = 1$
$ \Rightarrow 5 + 7x = 7$[By cross multiplication]
$ \Rightarrow 7x = 7 - 5$
$ \Rightarrow 7x = 2$
Therefore, required fraction = $\dfrac{2}{7}$

Therefore, Red roses in the garden =$\dfrac{2}{7}$

Note: We can solve the above question using Probability Distribution. Probability distributions indicate the likelihood of an event or outcome. The sum of all probabilities is equal to 1. No matter how a ratio is written, it is important that it can be simplified down to the smallest whole numbers possible, just as with any fraction.