Question

In isosceles trapezoid \[WTYH,WH||XZ||TY,m\angle TWH = 120,\] and \[m\angle HWE = 30\,.\,XZ\] passes through point \[E,\] the intersection of diagonals. If \[WH = 30\], determine the ratio of \[XZ:TY\].

A) \[1:2\]
B) \[2:3\]
C) \[3:4\]
D) \[4:5\]
E) \[5:6\]

Answer 1

Hint: In order to determine the ratio of \[XZ:TY\], we need to understand the properties of an isosceles trapezoid in which both legs and both base angles are of the same measure. In other words, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal length (properties shared with the parallelogram). The diagonals are also of equal length.

Complete step by step solution:
In the given problem, we need to draw a triangle and use \[30 - 60 - 90\] relationship as follows:
Draw a straight line from \[E\] to \[\overline {WH} \] with the foot of the line ending at \[A\] as follows:

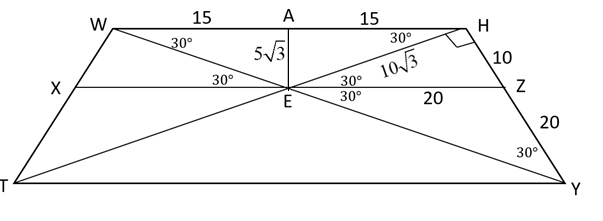
From the above figure we observe that \[\overline {AH} \]=\[15\]=\[\overline {AW} \] since it will be \[\dfrac{1}{2}\] \[\overline {WH} \] i.e. \[\dfrac{1}{2} \times 30 = 15\].
Now we can use the \[30 - 60 - 90\] relationship. A \[30 - 60 - 90\] triangle is a special right triangle whose angles are \[{30^ \circ }\], \[{60^ \circ }\], and \[{90^ \circ }\]. It is a matter of remembering the ratio of \[1:\sqrt 3 :2\] and knowing that the shortest side length is always opposite the shortest angle (\[{30^ \circ }\]) and the longest side length is always opposite the largest angle (\[{90^ \circ }\]).
Use the \[30 - 60 - 90\] relationship to determine that \[\overline {AE} \]=\[5\sqrt 3 \] and \[\overline {EH} \]=\[10\sqrt 3 \].
\[\Delta EHZ\] is also \[30 - 60 - 90\] triangle, so \[\overline {HZ} \]=\[10\] and \[\overline {EZ} \]=\[20\].
\[\Delta EYZ\] is an isosceles triangle making \[\overline {ZY} \]=\[20\].
In \[\Delta THY\], \[\overline {EZ} \] is parallel to \[\overline {TY} \], therefore, \[\dfrac{{HZ}}{{HY}} = \dfrac{{EZ}}{{TY}} = \dfrac{1}{3}\]
So we can conclude that \[\dfrac{{HZ}}{{TY}} = \dfrac{2}{3}\]
Hence, \[XZ:TY = 2:3\]. so option (B) is correct.

Note:
Any triangle of the form\[30 - 60 - 90\] can be solved without applying long-step methods such as the Pythagorean Theorem and trigonometric functions. Triangles with the same angle measures are similar, and their sides will always be in the same ratio to each other. Since the \[30 - 60 - 90\] triangle is a right triangle, then the Pythagorean theorem \[{a^2} + {b^2} = {c^2}\] is also applicable to the triangle.