Question

In how many ways can the letter of the word ‘STORY’ be arranged so that T and Y are always together.
A) 24
B) 30
C) 10
D) 48

Answer 1

Hint:In this problem we will arrange all the letters by taking T and Y as a single unit and after that we will find out the total possible arrangements of these two letters T and Y.

Complete step-by-step answer:
Given: we have given the word ‘STORY’ and out of this word we have to find out that in how many ways can the word ‘STORY’ be arranged while the letter T and V come together.
First, find the letters available in the given word which are 5.
Now, we will take the letter T and Y as a single unit.
So, the total number of letters present in the given word after taking the letter T and Y as a single unit.

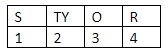
Now, that means there are 4 letters in the word.
So, total arrangements present in it is given by ${\text{N}}!$
Here ${\text{N}}$is the total units which are 4.
Then, substitute the value of ${\text{N}}$ in ${\text{N}}!$
$
  {\text{N}}! = 4! \\
   \Rightarrow 4 \times 3 \times 2 \times 1 \\
   \Rightarrow 24 \\
$
And now, we can arrange letters T and Y by $2!$ ways.
So, to get the total arrangements , we will multiply both the situations.
So, total arrangements is ,
Arrangements of 4 letters $ \times $arrangements of two letter T and Y.
That is ,$4! \times 2!$
Now, solve the equation.
$ = 24 \times 2 = 48$
So, the total ways of arrangements are 48 ways.
Hence, the option D is the correct answer.

Note:Make sure that you consider the alphabets T and Y as one single unit. Considering them as two separate units will lead to wrong answers. Also remember to see that the position of the alphabets is proper in such problems.