Question

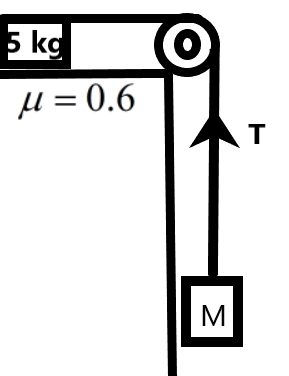
In given figure, the minimum value of ‘M’ such that 5 kg will move is –
                          

A) 1 kg
B) 2 kg
C) 3 kg
D) 4 kg

Answer 1

Hint: We need to understand the relation between the vertical force due to the gravitational force on the mass with the horizontal force due to the frictional force acting on the mass on the table. We can solve this by finding the proper relation between them.

Complete answer:
We know that a mass which is hung from a height has a force acting on it in the vertically downward direction due to the force of gravity. This force forms a tension on the string on which the mass is hung.
                                     

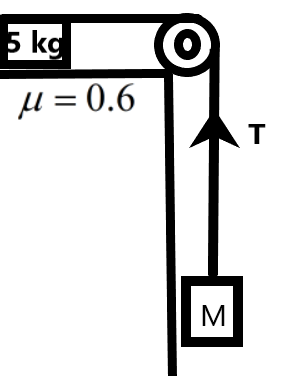
When another mass is attached to this string at the other end, then the tension will be felt by this mass. So, the tension on the string and the frictional force on the block on the table should be balanced for the masses to be at equilibrium. When the tension overcomes the frictional force then the masses start moving.
We can find the tension on the string from the given information as –
\[T=Mg\]
The frictional force acting on the mass of 5 kg placed on a table with coefficient of friction \[\mu \] is given as –
\[\begin{align}
  & F=\mu mg \\
 & \Rightarrow F=(0.6)(5)g \\
 & \therefore F=3gN \\
\end{align}\]
Now, we can equate the tension and the frictional force in the system to get minimum mass required to trigger motion in the system as –
\[\begin{align}
  & T={{F}_{f}} \\
 & \Rightarrow Mg=3g \\
 & \therefore M=3kg \\
\end{align}\]
 This is the required mass.

The correct answer is option C.

Note:
We have found the minimum mass which can cause motion in the system. This is also the maximum mass which can keep the block on the horizontal table to be at rest or it balances the frictional force acting on the mass on the table from slipping.