Question

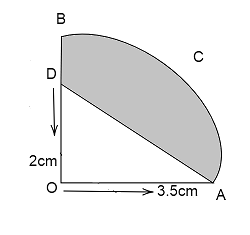
In figure,$ADBCA$ represents a quadrant of a circle of radius $3.5\,cm$ with center $O$. Calculate the area of the shaded portion (Take$\pi = \dfrac{{22}}{7}$)

A.$2.156\,c{m^2}$
B. $4.653\,c{m^2}$
C. $6.125\,c{m^2}$
D. None of the above.

Answer 1

Hint: We divide it into two simple geometrical figures, such as triangles, to determine the area of a quadrilateral. Then, using the formula, we find the area of the two separate triangles and add these areas to find the quadrilateral area. The opposite sides are parallel and the opposite angles are equal. The measurement is carried out in square units with a square meter standard unit.

Formula used:
Area of the quadrant is $\dfrac{1}{4}\pi {r^2}$
Where,
$r$ be the radius,
$\pi = \dfrac{{22}}{7}$
Area of the triangle is $\dfrac{1}{2} \times b \times h$
Where,
$b$ is base of the triangle,
$h$ is Height of the triangle
${\text{Area}}\,{\text{of}}\,{\text{the}}\,{\text{shaded}}\,{\text{region = Area}}\,{\text{of}}\,{\text{the}}\,{\text{quadrant - Area}}\,{\text{of}}\,{\text{the}}\,{\text{triangle}}\,$

Complete step-by-step answer:
Radius of the quadrant is $3.5\,cm$
Therefore, we Find Area of the quadrant $AOBCA$
The given formula
Area of the quadrant is $\dfrac{1}{4}\pi {r^2}$
Substituting the given value in above equation,
$r = 3.5,\pi = \dfrac{{22}}{7}$
We get,
$ \Rightarrow \dfrac{1}{4} \times \dfrac{{22}}{7} \times {\left( {3.5} \right)^2}$
On simplifying,
$ \Rightarrow 9.625$
Thus, the Area of the quadrant is $9.625$$c{m^2}$
Now,we find the Area of the triangle $AOD$
Area of the triangle is $\dfrac{1}{2} \times b \times h$
Where $b = OA,h = OD$
Substituting the above equation we get,
$ \Rightarrow \dfrac{1}{2} \times OA \times OD$
The corresponding values are $OA = 3.5,OD = 2$
Substituting the value,
$ \Rightarrow \dfrac{1}{2} \times 3.5 \times 2$
On simplifying,
We get,
$ \Rightarrow 3.5$
Thus,
The Area of triangle $AOD$is $3.5\,c{m^2}$
Then we find the Area of the shaded region
${\text{Area}}\,{\text{of}}\,{\text{the}}\,{\text{shaded}}\,{\text{region = Area}}\,{\text{of}}\,{\text{the}}\,{\text{quadrant - Area}}\,{\text{of}}\,{\text{the}}\,{\text{triangle}}\,\,{\text{AOD}}$
We know the value,
The Area of the quadrant is $9.625$$c{m^2}$
The Area of triangle $AOD$is $3.5\,c{m^2}$
Substituting the value in above equation, we get,
${\text{Area}}\,{\text{of}}\,{\text{the}}\,{\text{shaded}}\,{\text{region}} = 9.625 - 3.5$
On simplifying,
$ \Rightarrow 6.125$
Thus, the Area of the Shaded region is $6.125\,c{m^2}$
Hence,option C is the correct answer.

Note: A four-sided polygon is a quadrilateral, with the number of interior angles equal to 360o. All four angles are right angles within a rectangle. An analogous condition is that the diagonals bisect each other and are equal in length. Some of their sides and angles are equal in special forms of quadrilaterals.