Question

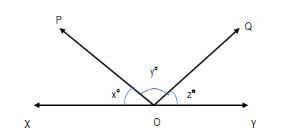
In figure, x:y:z=5:4:6. If XOY is a straight line, then the values of x, y and z are:

(a). $x=60{}^\circ $
(b). $y=48{}^\circ $
(c). $z=72{}^\circ $
(d). $z=80{}^\circ $

Answer 1

Hint: Think of the basic definition of ratio and use the fractional form of a ratio. Also, use the property that the angle on one side of a straight line is a straight angle, i.e., equal to $180{}^\circ $ .

Complete step-by-step answer:

Let us first know what a ratio is.
A ratio in basic words is a quantity used to define a comparison between two quantities. A bit toward the advanced side, it is the quantity that defines how many times of one quantity is that of others.
 At our level, apart from the definition, we will treat it as a simple fraction that defines a relation between two given quantities.
Now, starting with the solution to the above question. First, we will convert the ratio given in the question to the fractional form. On doing so, we get
x:y:z=5:4:6
$\dfrac{x}{y}=\dfrac{5}{4}..........(i)$
$\dfrac{z}{y}=\dfrac{6}{4}............(ii)$
Now we know that the angle on one side of a straight line is a straight angle, i.e., equal to $180{}^\circ $ .
$\therefore x+y+z=180$
If we take y common from the left-hand side of the equation, we get
$y\left( \dfrac{x}{y}+1+\dfrac{z}{y} \right)=180$
Now we will substitute the value $\dfrac{x}{y}$ and $\dfrac{z}{y}$ from equations (i) and (ii), respectively. On doing so, we get
 $y\left( \dfrac{5}{4}+1+\dfrac{6}{4} \right)=180$
$\Rightarrow y=\dfrac{180\times 4}{15}=48{}^\circ $
Now we will put the value of y in equation (i). On doing so, we get
$\dfrac{x}{48{}^\circ }=\dfrac{5}{4}$
$\Rightarrow x=60{}^\circ $
Again, if we substitute y in equation (ii), we get
$\dfrac{z}{48}=\dfrac{6}{4}$
$\Rightarrow z=72{}^\circ $
Therefore, the values of x, y and z are $60{}^\circ ,\text{ 48}{}^\circ \text{ and 72}{}^\circ $ , respectively. Hence, options (a), (b) and (c) are correct.

Note: Read the question carefully as in the question, including ratio, there is always a chance that the question might have a twist hidden in the words of the question. Also, while solving a fraction for finding the ratio, be sure that you convert it to the simplest form, i.e., the numerator and the denominator must not have any common factors.