Question

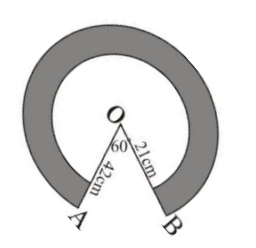
In figure two concentric circles with centre O, have radii $ 21\,\,cm $ and $ 42\,cm $ . If $ \angle AOB = {60^0} $ . Find the area of the shaded region. (Use $ \pi = \dfrac{{22}}{7} $ )

Answer 1

Hint: Firstly we calculate the major angle and using it we find the area of both sectors smaller and bigger. Then the difference of two area will give the area of the shaded region shown in figure.

Complete step-by-step answer:
On seeing the given figure we see that there are two sectors formed in the given figure.
One pair of sectors are considered as minor sectors of the circle, while the other pair of sectors are major sectors of the circle.
To find the area of a shaded region we find the area of a pair of major sectors of a given circle.
Therefore, for this we use major angle instead of minor angle given in figure.
Major angle of sector = total angle of circle – minor angle at centre
Major angle of sector = $ {360^0} - {60^0} = {300^0} $
Since, the circle is concentric therefore the angle for both major sectors will be the same.
But their radii will be different.
From the statement it is given that the radius of the smaller circle is $ 21\,\,cm $ and that of the bigger circle is $ 42\,cm $ .
Now, we will calculate area of both sectors
Area of bigger sector = $ \dfrac{\theta }{{{{360}^0}}} \times \pi {r^2},\,\,\,\,\,\,(\theta = {300^0},\,\,r = 42cm) $
\[
   \Rightarrow Area\,\,of\,\,bigger\,\,\sec tor = \dfrac{{300}}{{360}} \times \dfrac{{22}}{7} \times 42 \times 42 \\
   \Rightarrow Area\,\,of\,\,bigger\,\,\sec tor\,\, = 4620 \\
 \]
Therefore, from above we see that the area of the bigger sector is $ 4620\,\,c{m^2} $ .
Now, we will calculate the area of the smaller sector.
Area of smaller sector= $ \dfrac{\theta }{{{{360}^0}}} \times \pi {r^2},\,\,\,\,\,\,(\theta = {300^0},\,\,r = 21cm) $
\[
   \Rightarrow Area\,\,of\,\,smaller\,\,\sec tor = \dfrac{{300}}{{360}} \times \dfrac{{22}}{7} \times 21 \times 21 \\
   \Rightarrow Area\,\,of\,\,smaller\,\,\sec tor\,\, = 1155 \\
 \]
Therefore from above we see that the area of the smaller sector is $ 1155\,c{m^2} $ .
Now, to find the required shaded region we will subtract the area of the smaller sector from the area of the bigger sector.
Area of shaded region = $ 4620 - 1155 = 3465 $
Therefore, from above we see that area of shaded region is $ 3465\,c{m^2} $

Note: We can also find the answer to a given problem in another way. In this way we first calculate area of the ring formed by two concentric circles of given radii and then we calculate area of both minor sectors ( smaller and bigger) by using same formula mentioned above but for minor sectors we will take minor angle( $ {60^0} $ ) and subtract it from area of ring calculated earlier to find required shaded region.