Question

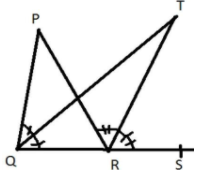
In Figure, the side QR of $\vartriangle PQR$ is produced to a point S. If the bisectors of $\angle PQR$ and $\angle PRS$ meet at point T, then prove that \[\angle {\mathbf{QTR}} = \dfrac{1}{2}\angle {\mathbf{QPR}}.\]
          

Answer 1

Hint: First we need to apply the relationship of exterior angle with the interior angles in the triangle TQR. Then apply the same relationship in triangle PQR. Use both equations with some transformations to get the result.

Complete step-by-step answer:
Line QR is extended till point S. It is given that bisectors of $\angle PQR$ and $\angle PRS$ meet at point T. Then two triangles will be $\vartriangle PQR$ and $\vartriangle TQR$.
Since the exterior angle of the triangle is equal to the sum of two opposite interior angles.
So, we will have first in $\vartriangle TQR$, having exterior angle TRS:
$\angle TRS = \angle TQR + \angle QTR$
Applying the transformation in above equation we get,
$\angle QTR = \angle TRS - \angle TQR$…(1)
Similarly in $\vartriangle PQR$, having exterior angle PRS:
$\angle PRS = \angle PQR + \angle QPR$….(2)
Since line TR is the bisector of $\angle PRS$. It means $\angle PRS = 2 \times \angle TRS$.
And line TQ is the bisector of $\angle PQR$. It means $\angle PQR = 2 \times \angle TQR$
So, in equation (2) by substituting above valueS , we get
$2\angle TRS = 2\angle TQR + \angle QPR$
$\angle QPR = 2\angle TRS - 2\angle TQR$….(3)
Dividing above equation by 2 on both sides in equation (3) , we get
$\dfrac{1}{2}\angle QPR = \angle TRS - \angle TQR$…(4)
Now by comparing equations (1) and (4), where both RHS are same, we get the equation as,
\[\angle {\mathbf{QTR}} = \dfrac{1}{2}\angle {\mathbf{QPR}}.\]
Hence we have proved the result.

Note: Geometry has many shapes which are having many theorems. These theorems are relating the sides and angles of those shapes. Many interesting results can be obtained from the given shape by using relevant theorems. Many real life problems are being solved with the help of geometrical theorems. In the above question two important theorems for triangles are used. Similarly for other problems we may apply many theorems. A careful visualization of the shape is very important for getting the correct result.