Question

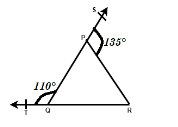
In figure, sides QP and QR of \[\Delta PQR\] are produced to points T and S respectively. If \[\angle TQP = 110^\circ \] and \[\angle SPR = 135^\circ \], then find the value of \[\angle PRQ\].

Answer 1

Hint:One sufficient information for solving this question is that the sum of all angles of a triangle is \[180^\circ \]. So, by using this concept we can solve for the value of \[\angle PRQ\]. We are going to apply the concept of linear pair (when a line intersects another line at an angle, the two angles formed make a linear pair, and the sum of the two angles of a linear pair is \[180^\circ \]).
So, first we are going to apply the concept of linear pair to the angle \[\angle SPR\] and then to the angle \[\angle TQP\] and find their corresponding linear pair and then use the angle sum property of triangle to solve for the value of \[\angle PRQ\].
Formula Used:
We are going to use the concept of angle sum property of a triangle – the sum of all angles of a triangle is \[180^\circ \], which hence, is:
\[\angle PQR + \angle QPR + \angle PRQ = 180^\circ \]

Complete step by step solution:
In this question, we need to solve for the value of \[\angle PRQ\] which is in the \[\Delta PQR\].
First, we calculate the other angles of the triangle. We have been given the value of \[\angle SPR\] and \[\angle TQP\] and we need to calculate the angles adjacent to them.
And we can easily do that by applying the concept of linear pair.
\[\angle SPR = 135^\circ \] and \[\angle TQP = 110^\circ \]
So, first we solve for \[\angle QPR\]:
\[\angle SPR + \angle QPR = 180^\circ \]
Hence, \[\angle QPR = 180^\circ - 135^\circ = 45^\circ \]
Now, we solve for \[\angle PQR\]
\[\angle TQP + \angle PQR = 180^\circ \]
Hence, \[\angle PQR = 180^\circ - 110^\circ = 70^\circ \]

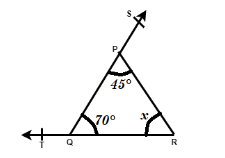
So, now we have two out of three angles of a triangle and we need to solve for the third unknown angle. And we can easily do that by applying the concept of the angle sum property, so we have:
\[\angle PQR + \angle QPR + \angle PRQ = 180^\circ \]
\[70^\circ + 45^\circ + x = 180^\circ \]
\[115^\circ + x = 180^\circ \]
\[x = 180 - 115 = 65^\circ \]
Hence, \[\angle PRQ = 65^\circ \]

Note: So, we saw that in solving questions like these, we need to see what information we have got with us. Like here, we used the concept of angle sum property of triangle, because the figure clearly gave a triangle. Then we applied the concept of linear pair, because the angles in the triangle which we needed to find for calculating the \[\angle PRQ\] and the angles whose measure is given lie on a straight line, hence forming a linear pair. The biggest giveaway is always what shape the figure is; we figure that out, we know in which direction we need to go.