Question

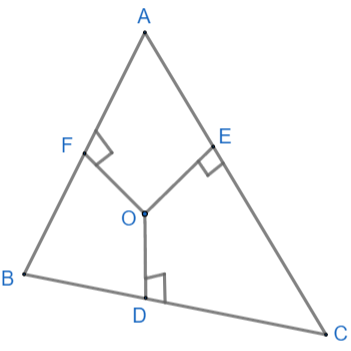
In figure, O is a point in the interior of a triangle ABC, $OD\bot BC,OE\bot AC\text{ and }OF\bot AB$ show that,
\[\begin{align}
  & \left( i \right)O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}-O{{D}^{2}}-O{{E}^{2}}-O{{F}^{2}}=A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}} \\
 & \left( ii \right)A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=A{{E}^{2}}+C{{D}^{2}}+B{{F}^{2}} \\
\end{align}\]

Answer 1

Hint: In this question, we will see that six right angled triangles are formed when O is taken in interior and $OD\bot BC,OE\bot AC,OF\bot AB$. We will use Pythagoras theorem in right angled triangles to prove required equations. Pythagoras theorem states that, sum of squares of perpendicular and base are equal to the square of hypotenuse, that is ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$ where H is hypotenuse, P is perpendicular and B is base.

Complete step-by-step answer:
We are given a triangle ABC and O is a point in the interior of a triangle ABC, where $OD\bot BC,OE\bot AC,OF\bot AB$
We have to prove that,
\[\begin{align}
  & \left( i \right)O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}-O{{D}^{2}}-O{{E}^{2}}-O{{F}^{2}}=A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}} \\
 & \left( ii \right)A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=A{{E}^{2}}+C{{D}^{2}}+B{{F}^{2}} \\
\end{align}\]
For solving, let us join the point O from A, B and C.

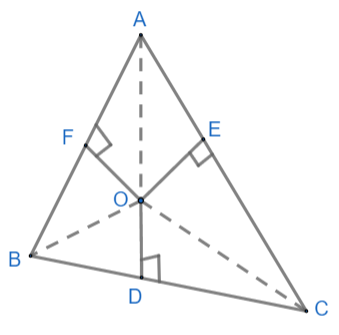
As we can see, we have obtained six right angled triangles which are \[\Delta BOD,\Delta BOF,\Delta OFA,\Delta OEA,\Delta OEC\text{ and }\Delta DOC\]
(i) Let us consider right angled triangles $\Delta OAF,\Delta ODB\text{ and }\Delta OEC$ for solving part (i)
From Pythagoras theorem, we know that ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$ where H is hypotenuse, P is perpendicular and B is base.
In a right angled triangle OAF.
\[{{\left( OA \right)}^{2}}={{\left( AF \right)}^{2}}+{{\left( OF \right)}^{2}}\cdots \cdots \cdots \cdots \left( 1 \right)\]
In a right angled triangle ODB.
\[{{\left( OB \right)}^{2}}={{\left( OD \right)}^{2}}+{{\left( BD \right)}^{2}}\cdots \cdots \cdots \cdots \left( 2 \right)\]
In a right angled triangle OEC.
\[{{\left( OC \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( EC \right)}^{2}}\cdots \cdots \cdots \cdots \left( 3 \right)\]
Let us now add (1), (2) and (3) to obtain the required result.
Adding (1), (2) and (3) we get:
\[O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}=A{{F}^{2}}+O{{F}^{2}}+O{{D}^{2}}+B{{D}^{2}}+O{{E}^{2}}+E{{C}^{2}}\]
Rearranging the terms, we get:
\[O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}-O{{D}^{2}}-O{{E}^{2}}-O{{F}^{2}}=A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}\]
Hence proved.
(ii) For (ii) part, we will take all six right angled triangles.
Using Pythagoras theorem ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$ where H is hypotenuse, P is perpendicular and B is base.
In the right angled triangle ODB.
\[\begin{align}
  & {{\left( OB \right)}^{2}}={{\left( OD \right)}^{2}}+{{\left( BD \right)}^{2}} \\
 & \Rightarrow {{\left( BD \right)}^{2}}={{\left( OB \right)}^{2}}-{{\left( OD \right)}^{2}}\cdots \cdots \cdots \cdots \left( 4 \right) \\
\end{align}\]
In the right angled triangle OFA.
\[\begin{align}
  & {{\left( OA \right)}^{2}}={{\left( OF \right)}^{2}}+{{\left( AF \right)}^{2}} \\
 & \Rightarrow {{\left( AF \right)}^{2}}={{\left( OA \right)}^{2}}-{{\left( OF \right)}^{2}}\cdots \cdots \cdots \cdots \left( 5 \right) \\
\end{align}\]
In the right angled triangle OEC.
\[\begin{align}
  & {{\left( OC \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( CE \right)}^{2}} \\
 & \Rightarrow {{\left( CE \right)}^{2}}={{\left( OC \right)}^{2}}-{{\left( OE \right)}^{2}}\cdots \cdots \cdots \cdots \left( 6 \right) \\
\end{align}\]
Adding (4), (5) and (6) we get:
\[\begin{align}
  & A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=\left( O{{A}^{2}}-O{{F}^{2}} \right)+\left( O{{B}^{2}}-O{{D}^{2}} \right)+\left( O{{C}^{2}}-O{{E}^{2}} \right) \\
 & \Rightarrow A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}-O{{F}^{2}}-O{{D}^{2}}-O{{E}^{2}}\cdots \cdots \cdots \left( 7 \right) \\
\end{align}\]
In the right angled triangle OFB.
\[\begin{align}
  & {{\left( OB \right)}^{2}}={{\left( OF \right)}^{2}}+{{\left( BF \right)}^{2}} \\
 & \Rightarrow {{\left( BF \right)}^{2}}={{\left( OB \right)}^{2}}-{{\left( OF \right)}^{2}}\cdots \cdots \cdots \cdots \left( 8 \right) \\
\end{align}\]
In the right angled triangle OEA.
\[\begin{align}
  & {{\left( OA \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( AE \right)}^{2}} \\
 & \Rightarrow {{\left( AE \right)}^{2}}={{\left( OA \right)}^{2}}-{{\left( OE \right)}^{2}}\cdots \cdots \cdots \cdots \left( 9 \right) \\
\end{align}\]
In the right angled triangle ODC.
\[\begin{align}
  & {{\left( OC \right)}^{2}}={{\left( OD \right)}^{2}}+{{\left( CD \right)}^{2}} \\
 & \Rightarrow {{\left( CD \right)}^{2}}={{\left( OC \right)}^{2}}-{{\left( OD \right)}^{2}}\cdots \cdots \cdots \cdots \left( 10 \right) \\
\end{align}\]
Adding (8), (9) and (10) we get:
\[\begin{align}
  & A{{E}^{2}}+C{{D}^{2}}+B{{F}^{2}}=\left( O{{A}^{2}}-O{{E}^{2}} \right)+\left( O{{C}^{2}}-O{{D}^{2}} \right)+\left( D{{B}^{2}}-O{{F}^{2}} \right) \\
 & \Rightarrow A{{E}^{2}}+C{{D}^{2}}+B{{F}^{2}}=O{{A}^{2}}+O{{B}^{2}}+O{{C}^{2}}-O{{F}^{2}}-O{{D}^{2}}-O{{E}^{2}}\cdots \cdots \cdots \left( 11 \right) \\
\end{align}\]
As we can see from (7) and (11), the right hand side is equal in both. Therefore,
\[A{{F}^{2}}+B{{D}^{2}}+C{{E}^{2}}=A{{E}^{2}}+C{{D}^{2}}+B{{F}^{2}}\]
Hence proved.

Note: Students should carefully apply Pythagoras theorem in all the triangles. Drawing figures helps us in understanding questions clearly. Calculation should be done carefully in these types of questions as there can be a lot of confusion in naming the sides of a triangle.