Question

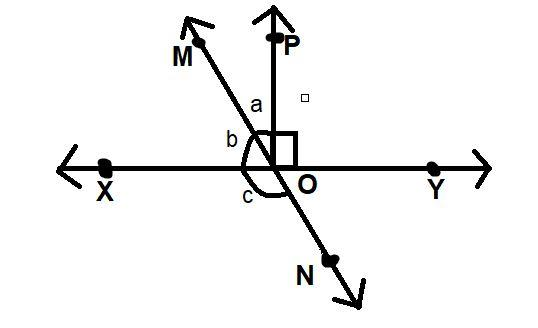
In figure, lines XY and MN intersect at O. If $\angle POY = {90^0}$ and a: b=2:3, find c.

Answer 1

Hint: Here we go through by applying the properties of supplementary angle, complementary angles and then assume the given ratio with some variable as we let a=2x and b=3x. then apply the condition of angle to find the unknown angle.

Complete step-by-step answer:
Here in the given question the ratio of angle a: b is given as 2:3. So we have to let the $\angle POM = a = 2x$ and $\angle MOX = b = 3x$.
Given $\angle POY = {90^0}$ ,
So,$\angle POX$ will be ${180^0}$-$\angle POY = {90^0}$ (Because $XOY$ is straight line)
Then $\angle POX$=$\angle POM$+$\angle MOX$=${90^0}$
And as we know that $\angle POM$ and $\angle MOX$ are complementary because the sum of these two angles is ${90^0}$. I.e. $\angle POM + \angle MOX = {90^0}$ after putting the values of these angle we get,
$
   \Rightarrow 2x + 3x = {90^0} \\
   \Rightarrow 5x = {90^0} \\
  \therefore x = {18^0} \\
 $
By putting the values of we get,
$\angle POM = a = 2 \times {18^0} = {36^0}$ And $\angle MOX = b = 3 \times {18^0} = {54^0}$
And we also know that $\angle MOX$ and $\angle XON$ are supplementary angles because the sum of these two angles is ${180^0}$. i.e. $\angle MOX + \angle XON = {180^0}$
$
   \Rightarrow {54^0} + \angle XON = {180^0} \\
   \Rightarrow \angle XON = {180^0} - {54^0} = {126^0} \\
 $
Hence the value of $\angle XON = c = {126^0}$.

Note: Whenever we face such a type of question the key concept for solving the question is to first determine which two angles are complementary and which two are supplementary and by putting the values of the angle in that values we will easily get the answer.