Question

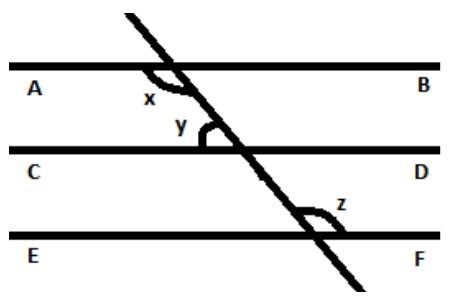
In figure, if $AB\parallel CD$, $CD\parallel EF$ and $y:z = 3:7$, find $x$.

Answer 1

Hint: In this question, we need to find the values of $x,y,z$. Here, we will determine the value of $y$ using the given condition $y:z = 3:7$. Then by using the concept of alternate interior angles and the sum of linear pairs, we will determine the values of $y$ and $z$. Then, by using the concept of sum of interior angles on the same side of transversal is supplementary, we will determine the value of $x$.

Complete step by step answer:
It is given that
$y:z = 3:7$
$ \Rightarrow \dfrac{y}{z} = \dfrac{3}{7}$
$ \Rightarrow y = \dfrac{3}{7}z$

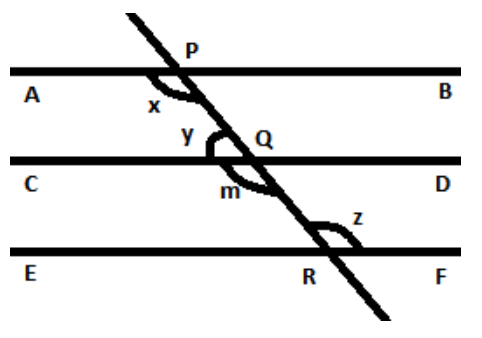
Let $\angle CQR = m$
Now, we know that $CD\parallel EF$. Then we know that the alternate interior angles are equal. Here $m$ and $z$ are alternate interior angles.
Therefore, $m = z$
Also, we know that the sum of linear pairs of angles is equal to $180^\circ $. Here, the angles $y$ and $m$ are in linear pairs.
Therefore, $y + m = 180^\circ $
As $m = z$,
$\Rightarrow y + z = 180^\circ $
Now, substituting $y = \dfrac{3}{7}z$, we have,
$\Rightarrow \dfrac{3}{7}z + z = 180^\circ $
$\Rightarrow \dfrac{{3z + 7z}}{7} = 180^\circ $
$\Rightarrow \dfrac{{10z}}{7} = 180^\circ $
$\Rightarrow z = \dfrac{7}{{10}} \times 180^\circ $
$\Rightarrow z = 126^\circ $
 Now, substituting $z = 126^\circ $ in $y = \dfrac{3}{7}z$,
$\Rightarrow y = \dfrac{3}{7} \times 126^\circ $
$\Rightarrow y = 54^\circ $
Also, we know that $AB\parallel CD$ and here, $PR$ is transversal.
As, we know that the sum of interior angles on the same side of transversal is supplementary, we have,
$\Rightarrow x + y = 180^\circ $
$\Rightarrow x + 54^\circ = 180^\circ $
$\Rightarrow x = 180^\circ - 54^\circ $
$\Rightarrow x = 126^\circ $ .

Hence, $x = 126^\circ $, $y = 54^\circ $ and $z = 126^\circ $.

Note: In this question it is important to note that alternate interior angles are formed when two parallel or non-parallel lines are intersected by a transversal. And also, the alternate interior angles are always equal. Here $m$ and $z$ are alternate interior angles. Then, the linear pair is a pair of angles that share a side and a base. Alternately, they are the two angles created along the line when two lines intersect. Here, the angle $y$ and $m$ are in the linear pair. However, we can determine $\angle x$ using the concept of alternate interior angles as $AB\parallel CD$, $CD\parallel EF$ which shows \[AB\parallel EF\]. Therefore, $x$ and $z$ are alternate interior angles. So, we can say $\angle x = \angle z = 126^\circ $.