Question

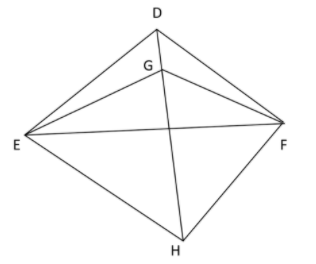
In figure, G is the point of concurrency of medians of $\vartriangle DEF$. Take point H on ray DG such that $DG = GH$. Then prove that quadrilateral GEHF is a parallelogram.

     

Answer 1

Hint: So here you need to prove parallelogram , so you must know the properties of parallelogram, that is, both diagonals of parallelogram bisect each other. You can use this property to prove the above equation.

Complete step-by-step answer:
So, basically, you are given a triangle $\vartriangle DEF$ in which G is concurrence of medians and when DG median is extended then locate a point H such that $DG = GH$ according to the question.
Here let us assume A be the point where median DG cuts EF.

          

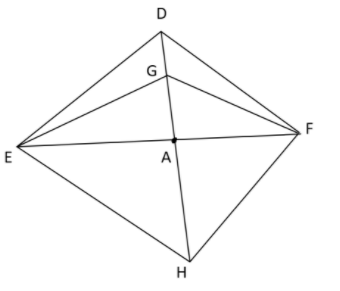
So, it is known that median bisects the side, therefore, A is the mid point of EF .So, we can write as
$AE = AF$ (1)
Now, secondly, we should know that the concurrence point of median, i.e., G.
So, let me clear the concurrence point of the median in a triangle.
If a median is drawn from each vertex in a triangle then each median intersects at a common point. Here it is G. So, this common point divides the median in the ratio $2:1$.
So, here, DA is median and G is the concurrence point of the median so G must intersect DA in the ratio $2:1$.
In mathematical form we can write as
$
  DG:GA = 2:1 \\
  \dfrac{{DG}}{{GA}} = \dfrac{2}{1} \\
  DG = 2AG \\
 $
$DG = 2AG$ (2)
And as we know that $DG = GH$ that is given in the question, we put the value of DG in the equation (1)
We got, $GH = 2AG$
It means A is the mid point of GH
Hence, $GA = AH$
Now, we know if diagonals bisect each other then quadrilateral must be parallelogram.
Here, let's see the quadrilateral GEHF.
Here, the diagonals GH and EF meet at point A.
And as we proved that A bisects GH and also we had proved that A is the mid point of EF.
Therefore, we can say that A bisects both diagonals. Therefore, it must be a parallelogram.

Note: In this question, you must remember that median bisects the sides and concurrence point of medians divide each median in $2:1$ ratio. Also you must remember that if diagonal bisects each other then the quadrilateral must be a parallelogram.