Question

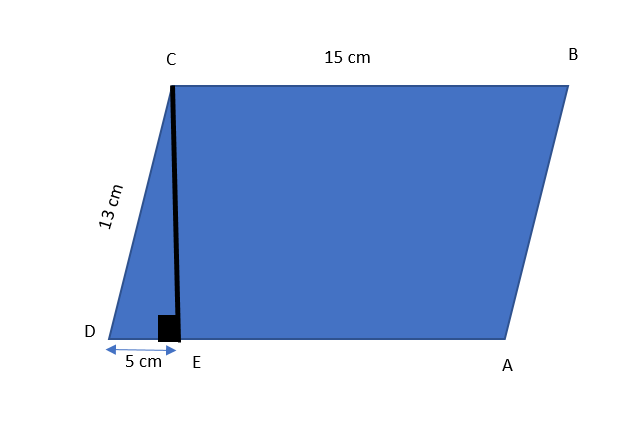
In figure, find the area of the parallelogram:

Answer 1

Hint: We will break down the given figure ABCD into two triangles and a rectangle. And then on using the formula for the area of the triangles and the area of rectangles, we will find the areas of those small parts and then sum them up to get the answer.

Step-By-Step answer:
We are given a parallelogram ABCD, where BC = 15 cm.
Since the opposite sides are equal to each other. So, AD = BC = 15 cm.
DE is given to be 5 cm.
Since AD = AE + ED
$ \Rightarrow 15 = AE + 5$
$ \Rightarrow AE = 10cm$ …………..(1)
Now, if a drop a perpendicular from A to the line BC cutting g it at the point F, we will get the following picture:-

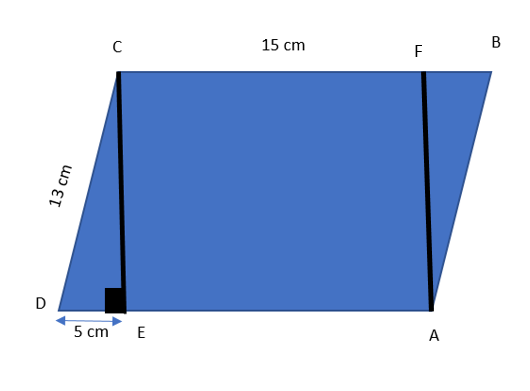
Now, we have two triangles named as CDE and ABF and a rectangle AFCE.
Now AE = FC = 10 cm.
In $\vartriangle CDE$:-
$ \Rightarrow C{D^2} = C{E^2} + D{E^2}$ (By Pythagorean Theorem)
$ \Rightarrow {13^2} = C{E^2} + {5^2}$
$ \Rightarrow C{E^2} = 169 - 25 = 144$
$ \Rightarrow CE = \pm 12$
Since, the length of the side cannot be negative. So, CE = 12 cm. ……………..(2)
We know that Area of a triangle is given by the following expression:-
$ \Rightarrow $ Area of a triangle = $\dfrac{1}{2} \times b \times h$
In $\vartriangle CDE$:-
$ \Rightarrow $ Area of a $\vartriangle CDE$= $\dfrac{1}{2} \times CE \times AE$ (By 1 and 2)
$ \Rightarrow $ Area of a $\vartriangle CDE$= $\dfrac{1}{2} \times 5 \times 12 = 30c{m^2}$ …………….(3) [Using equation 2]
Consider $\vartriangle CDE$ and $\vartriangle ABF$:-
$ \Rightarrow $ CE = AF (Perpendicular distance between two parallels is equal)
$ \Rightarrow $ CD = AB (Opposite sides of a parallelogram)
$ \Rightarrow \angle CED = \angle AFB$ (Both are right angles)
$\therefore \vartriangle CDE \cong \vartriangle ABF$ (By SAS congruence rule)
[SAS congruence rule: It states that if the two corresponding sides and one corresponding side of two triangles are equal, then the triangles are called as congruent triangles]
Now since these triangles are congruent, they are equal in area.$\therefore ar(\vartriangle CDE) = ar(\vartriangle ABF) = 30c{m^2}$ ……………….(4) [By equation 3]
Now, we know that the area of rectangle is given by the following expression:-
$ \Rightarrow $ Area of a rectangle = $length \times breadth$
In the rectangle AECF, we have:-
$ \Rightarrow $ Area of a rectangle AECF = $AE \times CE = 10 \times 12 = 120c{m^2}$ ………………..(5) [Using 1 and 2]
Now, area of ||gm ABCD = $ar\left( {\vartriangle CDE} \right) + ar\left( {\vartriangle ABF} \right) + ar\left( {\square AECF} \right)$
$ \Rightarrow $Area of ||gm ABCD $ = \left( {30 + 30 + 120} \right)c{m^2}$
$ \Rightarrow $Area of ||gm ABCD $ = 180c{m^2}$

Hence, the answer is 180 square cm.

Note: The students must note that they may skip the part when we proved the triangles to be congruent and directly use the formula for area of triangles in another triangle as well to find its area to be equal to 30 square cm.
The students must notice that we did break the figure, because we were already given a triangle in the parallelogram which made our job easy.
The students must commit to memory the following formulas:-
$ \Rightarrow $ Area of a rectangle = $length \times breadth$
$ \Rightarrow $ Area of a triangle = $\dfrac{1}{2} \times b \times h$