Question

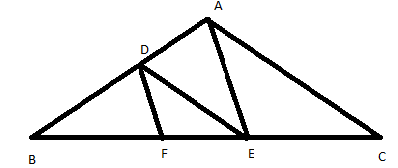
In figure, \[DE\parallel AC\] and \[DF\parallel AE\]. Prove that\[\dfrac{{BF}}{{FE}} = \dfrac{{BE}}{{EC}}\].

Answer 1

Hint: To solve this geometry, use a similar triangle concept.
Similar triangles, two figures having the same shape (but not necessarily the same size) are called similar figures.
The first part of the solution is important, for that, we use one of the theorems of a similar triangle that is, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Complete step-by-step answer:
Given: \[DE\parallel AC\] and \[DF\parallel AE\]
To prove: \[\dfrac{{BF}}{{FE}} = \dfrac{{BE}}{{EC}}\]
In a triangle \[ABC\]
We have to see that \[DE\parallel AC\] (Lines drawn parallel to one side of triangle intersects the other two sides in distinct points, and then it divides the other two side in same ratio)
Here, by the theorem, in a triangle \[ABC\] the line \[DE\] which is parallel to \[AC\] intersects the other two sides in distinct points, so it divides the other two side in same ratio

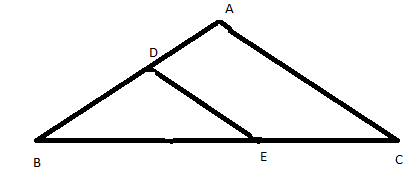
The ratio is
   \[\dfrac{{BE}}{{EC}} = \dfrac{{BD}}{{DA}}....\left( 1 \right)\]
Similarly, we can write
In a triangle \[AEB\],
\[DF\parallel AE\]
(Lines drawn parallel to one side of triangle intersects the other two sides in distinct points, then it divides the other two side in same ratio)
Here, by the theorem, in a triangle\[AEB\] the line \[DF\] which is parallel to \[AE\] intersects the other two sides in distinct points, so it divides the other two sides in the same ratio.

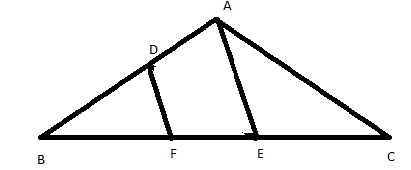
The ratio is
\[\dfrac{{BF}}{{FE}} = \dfrac{{BD}}{{DA}}....\left( 2 \right)\]
 The ratio of \[(1)\& (2)\] shows the two triangles \[ABC\ & AEB\], \[\angle ABC\] = \[\angle AEB\] also corresponding sides are same ratio \[\dfrac{{BE}}{{EC}} = \dfrac{{BD}}{{DA}}\]=\[\dfrac{{BF}}{{FE}} = \dfrac{{BD}}{{DA}}\]
Thus,
\[\dfrac{{BF}}{{FE}} = \dfrac{{BE}}{{EC}}\]
Hence proved

Note: The theorem we state is called basic proportionality theorem.
Two triangles are said to be similar, if their corresponding angles are equal and their corresponding sides are in the same ratio proportion.