Question

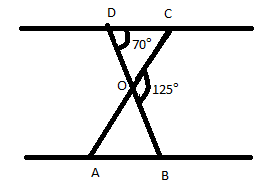
In figure \[\Delta ODC \sim \Delta OBA\], \[\angle BOC = {125^ \circ }\] and \[\angle CDO = {70^ \circ }\]. Find \[\angle DOC\], \[\angle DCO\] and \[\angle OAB\].
               

Answer 1

Hint: To solve this geometry, use a similar triangle concept. Similar triangles, two figures having the same shape (but not necessarily the same size) are called similar figures.
Two triangles are said to be similar, if
Their corresponding angles are equal and
Their corresponding sides are in the same ratio proportion.
We suppose to use the linear pair concept also, A linear pair of angles is formed when two lines intersect.
Use this definition to solve the sum

Complete step-by-step answer:
It is given that \[\Delta ODC \sim \Delta OBA\]
By definition of a similar triangle, their corresponding angles are equal.
\[\angle O = \angle O\]
\[\angle D = \angle B\]
\[\angle C = \angle A\]
From the figure, we obtained \[\angle D = {70^ \circ }\]
Therefore, \[\angle B = {70^ \circ }\](\[\angle OBA = {70^ \circ }\])
Now, consider \[BD\] is a line, so consider linear pair (A linear pair is a pair of adjacent angles formed when two lines intersect, that is, \[\angle BOC\] is intersect with \[\angle DOC\], the measure of the straight angle is \[{180^ \circ }\], so a linear pair of angles must add up to \[{180^ \circ }\] ).
\[\angle BOC + \angle DOC = {180^ \circ }\]
It is clearly known by see the below figure,
               

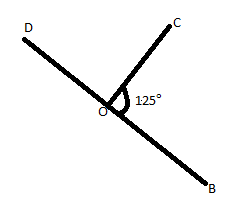
\[{125^ \circ } + \angle DOC = {180^ \circ }\]
\[\angle DOC = {180^ \circ } - {125^ \circ }\]
\[\angle DOC = {55^ \circ }\]
               

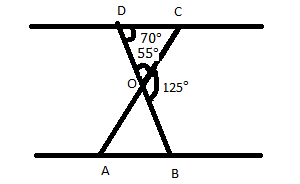
Now, in \[\Delta DCO\]
We know that the sum of all angles of triangles in \[{180^ \circ }\]
\[\angle CDO + \angle DCO + \angle DOC = {180^ \circ }\]
\[\angle CDO = {70^ \circ }\]
\[\angle DOC = {55^ \circ }\]
\[{70^ \circ } + \angle DCO + {55^ \circ } = {180^ \circ }\]
\[{125^ \circ } + \angle DCO = {180^ \circ }\]
\[\angle DCO = {180^ \circ } - {125^ \circ }\]
\[\angle DCO = {55^ \circ }\]
Now to find, \[\angle OAB\]
Given that,\[\Delta ODC \sim \Delta OBA\]
By using similar triangle concept, corresponding angles are equal
\[\angle O = \angle O\]
\[\angle D = \angle B\]
\[\angle C = \angle A\]
Then,
\[\angle O = {55^ \circ }\]
\[\angle D = {70^ \circ }\]
\[\angle C = {55^ \circ }\]
Thus, \[\angle A = {55^ \circ }\](that is,\[\angle DCO = \angle OAB\])
Hence \[\angle OAB = {55^ \circ }\]
Thus, we end up with\[\angle DOC = {55^ \circ }\],\[\angle DCO = {55^ \circ }\]\[\angle OAB = {55^ \circ }\]

Note: If two triangles are said to be similar,” corresponding angles of similar triangles are equal”.
Here, almost use the first concept of the similar triangle,
Although we have two conditions, it is not mandatory to use the second condition. Because the sum is about the angles of the triangle.
Suppose, if the question is related to corresponding sides as well as corresponding angles, we may definitely use the both conditions of the similar triangles.