Question

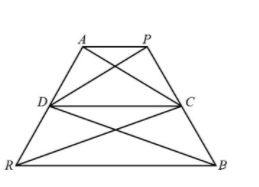
In figure, $ar(DRC) = ar(DPC)$ and $ar(BDP) = ar(ARC)$. Show that both the quadrilaterals ABCD and DCPR are trapeziums.
                                                   

Answer 1

Hint: Here, we will use the property of triangle which states that if two triangles lying on the same base have the same area then they both lie between a pair of parallel lines.

Complete step-by-step solution:
Given:
The area of the triangle is equal to $ar(DRC) = ar(DPC)$.
The area of the triangle is equal to $ar(BDP) = ar(ARC)$.
Since, DRC and DPC are two triangles of the same area and lie on the same base CD then$PR\parallel CD$.
Hence, DCPR is a trapezium.
Now, in relation $ar(BDP) = ar(ARC)$ subtract $ar(DRC)$ from both sides.
$\begin{array}{l}
ar(BDP) - ar(DRC) = ar(ARC) - ar(DRC)\\
ar(BDP) - ar(DPC) = ar(ARC) - ar(DRC)
\end{array}$
Since, $ar(DRC) = ar(DPC)$
So,$ar(BDC) = ar(ACD)$
Since, BDC and ACD are two triangles of the same area and lie on the same base CD then$AB\parallel CD$.
Hence, ABCD is a trapezium.

Note: The condition to obtain a trapezium from a triangle is that the area of two triangles should be equal and they should lie on the same base between two parallel lines.