Question

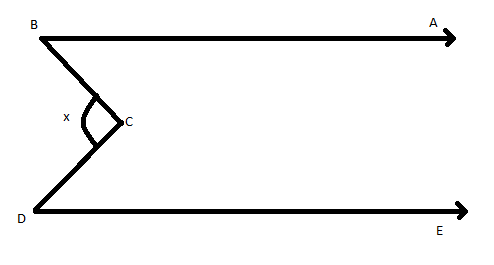
In figure, $AB\parallel ED$and \[\angle ABC = 30^\circ \], \[\angle EDC = 70^\circ \], then find the value of x.

Answer 1

Hint: We can draw a line passing through C, parallel to the parallel lines. This divides the angle into two parts. Then using the concept of parallel lines intersected by a transversal, we can find the measure of each part of the angle. Then we get the value of x by adding them.

Complete step by step answer:

We can draw the figure given in the question. As $AB\parallel ED$, and then draw a line PQ parallel to AB and ED.

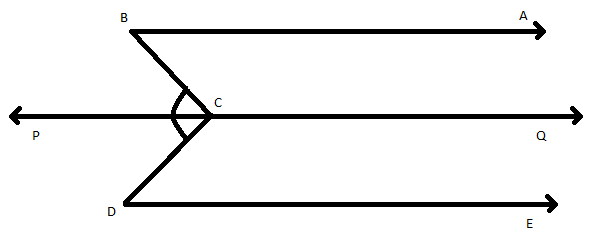
We can draw the figure given in the question. As $AB\parallel ED$, we can draw line PQ parallel to AB and ED.
We need to find x. It is the measure of angle BCD.
From the figure, the line PQ divides $\angle BCD$ into two parts. So, we can write,
$\angle BCD = \angle BCP + \angle PCD$.. (1)
Now we can consider the parallel lines AB and PQ. It is cut by the transversal BC.
From the figure, we can say that the $\angle ABC$ and $\angle BCP$ are alternate interior angles. We know that alternate interior angles when 2 parallel lines are intersected by a transversal are equal.
$ \Rightarrow \angle ABC = \angle BCP$
It is given that, \[\angle ABC = 30^\circ \].
\[ \Rightarrow \angle BCP = 30^\circ \] … (2)
Now we can consider the parallel lines DE and PQ. It is cut by a transversal CD.
Here, $\angle EDC$ and $\angle DCP$ are alternate interior angles. We know that alternate interior angles when 2 parallel lines are intersected by a transversal are equal.
 $ \Rightarrow \angle EDC = \angle DCP$
But it is given that, \[\angle EDC = 70^\circ \]
 $ \Rightarrow \angle DCP = 70^\circ $… (3)
On substituting (2) and (3) in (1), we get,
 $ \Rightarrow \angle BCD = 30^\circ + 70^\circ $
 $ \Rightarrow \angle BCD = 100^\circ $
 $ \Rightarrow x = 100^\circ $
Therefore, value of x is $100^\circ $.
Note: Alternate solution is given by, in the given figure We can join the points B and D to form a triangle BCD.

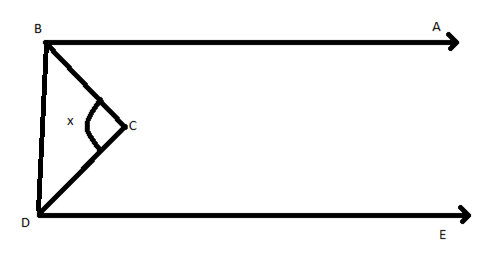
By angle sum property, $\angle BDC + \angle DBC + x = 180^\circ $…(a)
As AB and DE are parallel and BD is intersected, $\angle ABD$ and $\angle BDE$ are the alternate interior angles and they are supplementary.
 $ \Rightarrow \angle ABD + \angle BDE = 180^\circ $
From the figure we say that, $\angle ABD = \angle ABC + \angle CBD$ and $\angle BDE = \angle CDE + \angle BDC$.
 $ \Rightarrow \angle ABC + \angle CBD + \angle CDE + \angle BDC = 180^\circ $
It is given that, \[\angle ABC = 30^\circ \] and \[\angle EDC = 70^\circ \]
 $ \Rightarrow 30^\circ + \angle CBD + 70^\circ + \angle BDC = 180^\circ $
On rearranging, we, get.
 \[ \Rightarrow \angle CBD + \angle BDC = 180^\circ - 30^\circ - 70^\circ \]
 \[ \Rightarrow \angle CBD + \angle BDC = 80^\circ \] .
On substituting this in (a), we get,
 $80^\circ + x = 180^\circ $
 $ \Rightarrow x = 180^\circ - 80^\circ $
 $ \Rightarrow x = 100^\circ $
Therefore, value of x is $100^\circ $