Question

In figure ABCDE, find $\angle 1+\angle 2+\angle 3+\angle 4+\angle 5$.

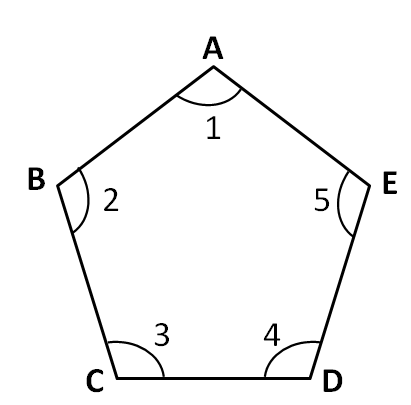
Answer 1

Hint: The angles in the sum given in the above question are the interior angles of the pentagon. To find the sum, we need to use the property that the sum of all the exterior angles of a polygon is always equal to ${{360}^{\circ }}$. Also since an exterior angle and the adjacent interior angle together form a linear pair, their sum will be equal to \[{{180}^{\circ }}\]. Using these we can determine the required sum asked in the above question.

Complete step-by-step solution:
Let us consider all of the exterior angles of the pentagon given in the above question in the below figure.

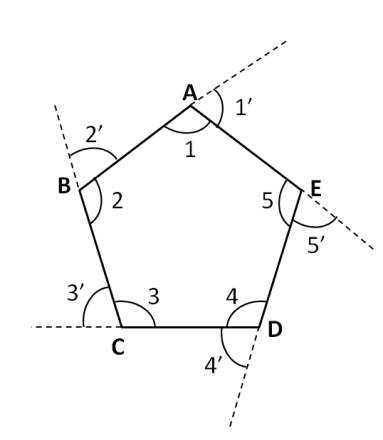
Now, we know that the sum of the exterior angles of any polygon is equal to ${{360}^{\circ }}$. So from the above figure, we can write
$\Rightarrow \angle 1'+\angle 2'+\angle 3'+\angle 4'+\angle 5'={{360}^{\circ }}........(i)$
Now, as can be seen in the above figure, the angles $\angle 1$ and $\angle 1'$ are forming a linear pair. So we can write
\[\begin{align}
  & \Rightarrow \angle 1'+\angle 1={{180}^{\circ }} \\
 & \Rightarrow \angle 1'={{180}^{\circ }}-\angle 1........(ii) \\
\end{align}\]
Similarly, we can have the following equations
\[\begin{align}
  & \Rightarrow \angle 2'={{180}^{\circ }}-\angle 2........(iii) \\
 & \Rightarrow \angle 3'={{180}^{\circ }}-\angle 3........(iv) \\
 & \Rightarrow \angle 4'={{180}^{\circ }}-\angle 4........(v) \\
 & \Rightarrow \angle 5'={{180}^{\circ }}-\angle 5........(vi) \\
\end{align}\]
Adding the equations (ii), (iii), (iv), (v), and (vi) we get
\[\begin{align}
  & \Rightarrow \angle 1'+\angle 2'+\angle 3'+\angle 4'+\angle 5'=5\left( {{180}^{\circ }} \right)-\left( \angle 1+\angle 2+\angle 3+\angle 4+\angle 5 \right) \\
 & \Rightarrow \angle 1'+\angle 2'+\angle 3'+\angle 4'+\angle 5'={{900}^{\circ }}-\left( \angle 1+\angle 2+\angle 3+\angle 4+\angle 5 \right) \\
 & \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5={{900}^{\circ }}-\left( \angle 1'+\angle 2'+\angle 3'+\angle 4'+\angle 5' \right) \\
\end{align}\]
Substituting the equation (i) in the above equation, we get
\[\begin{align}
  & \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5={{900}^{\circ }}-{{360}^{\circ }} \\
 & \Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5={{540}^{\circ }} \\
\end{align}\]
Hence, the given sum $\angle 1+\angle 2+\angle 3+\angle 4+\angle 5$ is equal to \[{{540}^{\circ }}\].

Note: We can also solve this question by using the formula for the sum of the interior angles of a polygon, which is given by \[\left( n-2 \right){{180}^{\circ }}\], where $n$ is the number of sides of the polygon. Since in the above question a pentagon is given to us, so on substituting $n=5$ in the formula, we will get the required sum as \[\left( 5-2 \right){{180}^{\circ }}={{540}^{\circ }}\] directly. Further, we can also divide the given pentagon into three triangles and apply the angle sum property to each to get the required sum.