Question

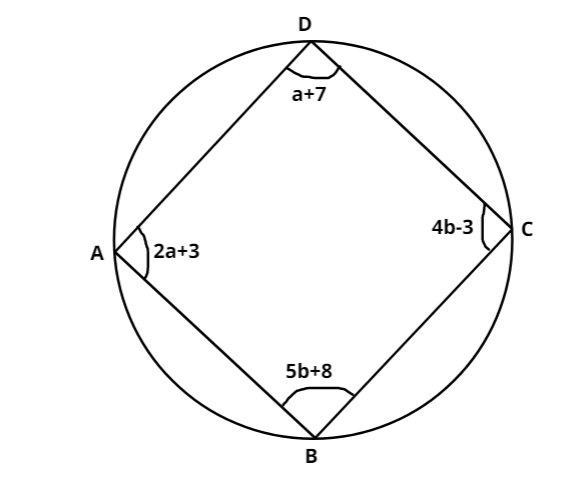
In figure, $ABCD$ is a cyclic quadrilateral. Find the values of a and b.

Answer 1

Hint: In order to solve this we have to apply the concept that the opposite angles of a cyclic quadrilateral are supplementary, that is, they are equal to $180_{}^\circ$.
Then we can simplify the data and get the required answer.

Complete step-by-step answer:
Since the opposite angles of a cyclic quadrilateral equals to $180_{}^\circ$.
From the above diagram we can write-
$\angle A = 2a + 3$,$\angle B = 5b + 8$,$\angle C = 4b - 3$ and $\angle D = a + 7$
Since the opposite angles of a cyclic quadrilateral equals to $180_{}^\circ$.
Therefore we can write-
$\angle B + \angle D = 180_{}^\circ$………...$(i)$
$\angle A + \angle C = 180_{}^\circ$…….....$(ii)$
Now by substituting the values of $\angle B$ and $\angle D$ in equation $(i)$ we get-
$\Rightarrow$$5b + 8 + a + 7 = 180_{}^\circ$
Now add the terms $8$ and $7$, moving on the right hand side we get-
$\Rightarrow$$a + 5b = {180^ \circ } - 15$
So, $a + 5b = 165_{}^\circ$………...$(iii)$
Again by substituting the values of $\angle A$ and $\angle C$ in equation $(ii)$ we get-
$\Rightarrow$$2a + 3 + 4b - 3 = 180$
So, $2a + 4b = 180$…………..…$(iv)$
Now by multiplying equation$(iii)$ by $2$ we get-
$\Rightarrow$$2a + 10b = 330$……….…$(v)$
Now by multiplying equation $(iv)$ by $1$ we get-
$\Rightarrow$$2a + 4b = 180$…….….$(vi)$
By applying elimination method on equation $(v)$ and $(vi)$ we get-
$\Rightarrow$$6b = 150$
By division we get-
$\Rightarrow$So, $b = \dfrac{{150}}{6} = 25$
Putting the value of $b$ in equation $(vi)$ we get-
$\Rightarrow$$2a + 4 \times 25 = 180$
On multiplying the terms we get,
$\Rightarrow$$2a + 100 = 180$
Moving $100$on the right hand side we get-
$\Rightarrow$$2a = 180 - 100$
By division we get-
$\Rightarrow$$a = \dfrac{{80}}{2} = 40$

Hence, the required values of $a$ and $b$ are $25_{}^\circ$ and $40_{}^\circ$

Note: A cyclic quadrilateral is a quadrilateral that has a circle lying on all its four vertices. Often it is called the inscribed quadrilateral, too.
The total of a pair of opposite angles is $180_{}^\circ$ in a cyclic quadrilateral.
The four vertices of the cyclic quadrilateral lie on the circumference of the circle.
If it is a cyclic quadrilateral, then it is necessary that the perpendicular bisectors must be concurrent.
The four perpendicular bisectors of the given four sides meet at the centre in a cyclic quadrilateral.