Question

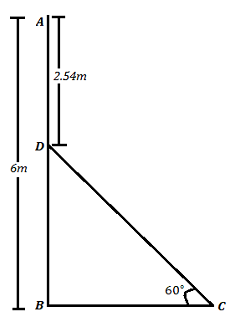
In Figure, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of the pole. If AD = 2.54 m, find the length of the ladder.

Answer 1

Hint: To solve the problems like this we have to find unknowns using trigonometric operations. In this problem we can take the triangle BCD and using the trigonometric functions we can solve for unknowns with substitution of the known values. This way the length of the ladder can be determined.

Complete step-by-step solution:
From the values given in the figure,
AD = 2.54 m
We can observe that,
AB = AD \[+\] DB = 6 m
So on substitution of AD in this equation we get,
\[\Rightarrow \] 2.54 m \[+\] DB = 6 m
\[\Rightarrow \] DB = 3.46 m
Now, in the right triangle BCD,
\[\dfrac{BD}{CD}=\sin {{60}^{\circ }}\]
\[\Rightarrow \]\[\dfrac{3.46m}{CD}=\dfrac{\sqrt{3}}{2}\]
We can substitute the value of \[\sqrt{3}\] as 1.73.
\[\Rightarrow \]\[\dfrac{3.46m}{CD}=\dfrac{1.73}{2}\]
Now let’s equate the equality to CD, so we get,
\[\Rightarrow \]\[CD=\dfrac{2\times 3.46m}{1.73}\]
On solving above RHS we get the value of CD as below,
\[\Rightarrow \] CD = 4m
Thus, the length of the ladder CD in the given figure is 4 m

Note: It is necessary for students to have the knowledge of trigonometric functions to determine the length of the ladder. Students can go wrong in substitution of the standard trigonometric values and even in the simplification part as there is a root term in the equation.