Question

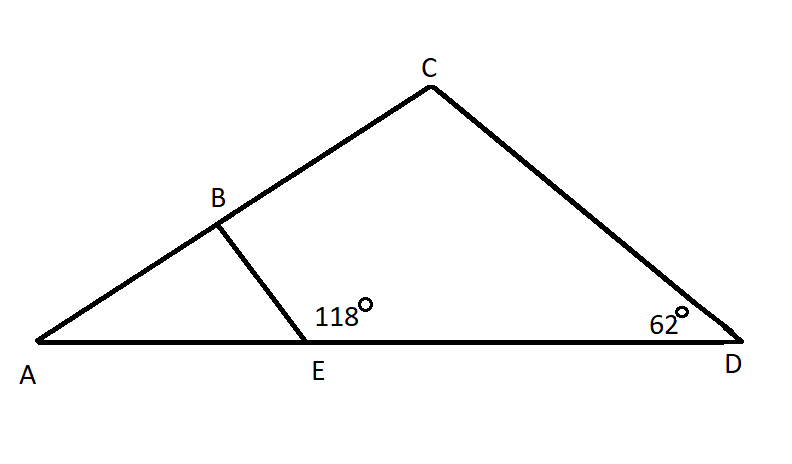
In Figure \[AB = BC\] , If the area of $\Delta ABE$ is x, Calculate the area of $\Delta ACD$

A.$x\sqrt 2 $
B.$x\sqrt 3 $
C.$2x$
D.$3x$

Answer 1

Hint: The given question refers to the concept of triangle and in particular it belongs to the similarity of triangle. To find the area of required triangle, first we will find $\angle BEA$ then using rules of similarity, we will prove $\Delta ABE \sim \Delta ACD$, then we will find the value of $A\left( {\Delta ACD} \right)$.

Complete step-by-step answer:
Here we have given that
\[AB{\text{ }} = {\text{ }}BC\]
$\angle BED = 118^\circ $ (Given)
So AB and AC are in the ratio 1:2 _ (I)
$\therefore \angle BED + \angle BEA = 180^\circ $ (linear pair)
$\therefore 118^\circ + \angle BEA = 180^\circ $
$\therefore \angle BEA = 62^\circ = \angle CDA$ _ (II)
In $\Delta ABE$ and $\Delta ACD$
Here $\angle A$ is the common angle.
$\therefore \angle BEA = \angle CDA$ From (II)
$\Delta ABE \sim \Delta ACD$ (AAA congruence)
\[\therefore \dfrac{{A(\Delta ABE)}}{{A(\Delta ACD)}} = {\left( {\dfrac{{AB}}{{AC}}} \right)^2}\] (Areas of similar triangles)
$ \to \dfrac{{A(\Delta ABE)}}{{A(\Delta ACD)}} = {\left( {\dfrac{1}{2}} \right)^2}$
$ \to \dfrac{x}{{A(\Delta ACD)}} = \dfrac{1}{4}$
$\therefore A(\Delta ACD) = $4x sq. units
$\therefore $The area of $\Delta ACD$ is 4x sq.units

Note: We can easily solve this type of questions using rules of similarity of triangles. Where similarity of triangles can be stated as “Triangles with the same shape and different size”. For example, in the following figure $\Delta ABC$ and $\Delta PQR$ both are equilateral triangles but different in size.