Question

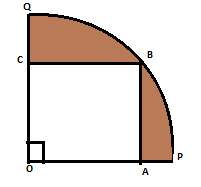
In figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA= 21 cm, find the area of the shaded region.

Answer 1

Hint: Here, first of all we will try to find out the radius of the circle whose quadrant is given. Then, to find the area of the shaded region, we can subtract the area of the square from the area of the quadrant.

Complete step-by-step answer:

Since, it is given that the length of OA = 21 cm.
It means that the length of the side of the square is 21 cm.
We can see that the length of OB will be the radius of the circle whose quadrant is given.
Since, OABC is a square. So, OB is the diagonal of this square.
We know that for any square of side length s, length of its diagonal is = $\sqrt{2}\times s$
So, from this formula length of the diagonal OB of the square OABC will be = $\sqrt{2}\times 21=1.41\times 21=29.6$
So, the length of OB is = 29.6 cm .
It means that the radius of the circle whose quadrant is given will also be = 29.6 cm.
Now, the area of the shaded region will be given as:
A = area of quadrant – area of the square………(1)
We know that the formula for area of a quadrant of a circle is = $\dfrac{1}{4}\times \pi \times {{r}^{2}}$
Also, the formula for the area of square is = ${{\left( side \right)}^{2}}$
On using these formulas with given values in equation (1), we get the area of shaded region as:
$\begin{align}
  & A=\dfrac{\pi {{r}^{2}}}{4}-{{\left( OA \right)}^{2}} \\
 & \Rightarrow A=\dfrac{22\times {{\left( 29.6 \right)}^{2}}}{7\times 4}-{{\left( 21 \right)}^{2}} \\
 & \Rightarrow A=\left( \dfrac{1}{4}\times \dfrac{22}{7}\times 882 \right)-441 \\
 & \Rightarrow A=693-441=252c{{m}^{2}} \\
\end{align}$
Hence, the area of the shaded region is $252c{{m}^{2}}$.

Note: Students should note here that the radius of a circle is the distance from its centre to its boundary. So, in this problem OB is the radius of the circle and it is also the diagonal of the square.