Question

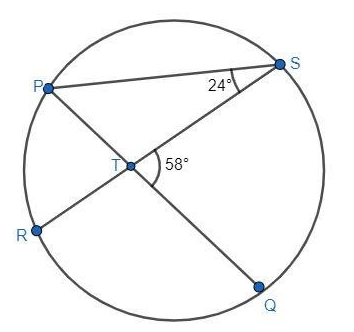
In figure 3.52, chords PQ and RS intersect at T.
1) Find \[m\left( {arc{\text{ SQ}}} \right)\] if \[m\angle {\text{STQ}} = {58^ \circ }\], \[m\angle {\text{PSR}} = {24^ \circ }\] .
2) Verify \[\angle {\text{STQ}} = \dfrac{1}{2}\left[ {m\left( {{\text{arc PR}}} \right) + m\left( {{\text{arc SQ}}} \right)} \right]\] .
3) Prove that \[\angle {\text{STQ}} = \dfrac{1}{2}\left[ {m\left( {{\text{arc PR}}} \right) + m\left( {{\text{arc SQ}}} \right)} \right]\]for any measure of \[\angle {\text{STQ}}\] .
4) Write in words the property in (3).

Answer 1

Hint:
Here we will find \[m\angle {\text{SPQ}}\] by using exterior angle theorem on \[\Delta TPS\]. Then, we will find \[m\left( {arc{\text{ SQ}}} \right)\] by using the inscribed angle theorem. We will find \[m\left( {{\text{arc PR}}} \right)\] using an inscribed angle theorem. Then, we will substitute the values of \[\angle {\text{STQ}}\], \[m\left( {{\text{arc PR}}} \right)\]and \[m\left( {{\text{arc SQ}}} \right)\]on the L.H.S and the R.H.S and verify the equation. We will prove the equation by using the exterior angle theorem on \[\Delta TPS\] and the inscribed angle theorem. We will state the property we have proved in the third part.

Complete step by step solution:

1) Let us apply the exterior angle theorem in \[\Delta TPS\]. According to it, the measure of the exterior angle of a triangle is equal to the sum of 2 interior opposite angles.
\[\begin{array}{l}\angle SPT + \angle PST = \angle STQ\\ \Rightarrow \angle SPT + 24^\circ = 58^\circ \end{array}\]
Subtracting both side by 24, we get
\[\begin{array}{l} \Rightarrow \angle SPT = 58^\circ - 24^\circ \\ \Rightarrow \angle SPT = 34^\circ \end{array}\]
Now, we will apply the inscribed angle theorem in. According to it, the measure of an inscribed angle in the circle is half the measure of the corresponding arc.
\[\begin{array}{l}m\left( {\angle SPQ} \right) = \dfrac{1}{2}m\left( {arc{\text{ SQ}}} \right)\\ \Rightarrow 34^\circ = \dfrac{1}{2}m\left( {arc{\text{ SQ}}} \right)\\ \Rightarrow 34^\circ \times 2 = m\left( {arc{\text{ SQ}}} \right)\\ \Rightarrow 68^\circ = m\left( {arc{\text{ SQ}}} \right)\end{array}\]
2) We will now apply the inscribed angle theorem. According to the theorem, the measure of an inscribed angle in a circle is half the measure of the corresponding arc.
\[\begin{array}{l} \Rightarrow \angle PSR = \dfrac{1}{2}m\left( {{\text{arc PR}}} \right)\\ \Rightarrow 24^\circ = m\left( {{\text{arc PR}}} \right)\\ \Rightarrow 24^\circ \times 2 = m\left( {{\text{arc PR}}} \right)\\48^\circ = m\left( {{\text{arc PR}}} \right)\end{array}\]
Let us verify the given equation.
L.H.S:
\[\angle STQ = {58^ \circ }\] (given)
R.H.S:
\[\begin{array}{l}\dfrac{1}{2}\left[ {m\left( {{\text{arc PR}}} \right) + m\left( {{\text{arc SQ}}} \right)} \right] = \dfrac{1}{2}\left[ {48^\circ + 68^\circ } \right]\\\Rightarrow \dfrac{1}{2}\left[ {116^\circ } \right]\\ \Rightarrow {58}^\circ \end{array}\]
We can observe that \[{\text{L}}{\text{.H}}{\text{.S}} = {\text{R}}{\text{.H}}{\text{.S}}\] , Hence we have verified the given equation and it is correct.
3) Let us apply the exterior angle theorem in \[\Delta TPS\]. According to it, the measure of the exterior angle of a triangle is equal to the sum of 2 interior opposite angles.

\[\begin{array}{l} \Rightarrow \angle SPT + \angle PST = \angle STQ\\ \Rightarrow \angle SPQ + \angle PSR = \angle STQ\end{array}\]
Now, let us apply the inscribed angle theorem on \[\angle SPQ\] and \[\angle PSR\]. According to it, the measure of an inscribed angle in a circle is half the measure of the corresponding arc.
\[\begin{array}{l}m\left( {\angle PSR} \right) = \dfrac{1}{2}m\left( {{\text{arc PR}}} \right)\\ \Rightarrow m\left( {\angle SPQ} \right) = \dfrac{1}{2}m\left( {arc{\text{ SQ}}} \right)\end{array}\]
Let us substitute these values in the equation.
\[\begin{array}{l}\angle SPQ + \angle PSR = \angle STQ\\ \Rightarrow \dfrac{1}{2}m\left( {{\text{arc SQ}}} \right) + \dfrac{1}{2}m\left( {{\text{arc PR}}} \right) = \angle STQ\\ \Rightarrow \dfrac{1}{2}\left[ {m\left( {{\text{arc SQ}}} \right) + m\left( {{\text{arc PR}}} \right)} \right] = \angle STQ\end{array}\]
We have obtained the desired result.
4) If 2 chords of a circle intersect inside it, the measure of angle between them is half the sum of measures of the arcs corresponding to the angle and its opposite angle.

Note:
\[\angle SPT\] and \[\angle SPQ\] represent the same angle and \[\angle PSR\] and \[\angle PST\] also represent the same angle. When we apply the inscribed angle theorem, we should be careful that the arc that is directly opposite to the inscribed angle should be used and not any other arc. We must not get confused between different properties of a circle.