Question

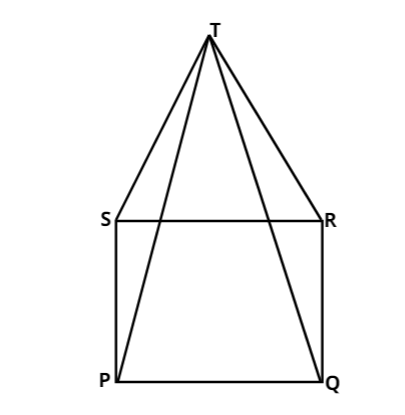
In fig, PQRS is a square and SRT is an equilateral triangle. Prove that PT=QT.

Answer 1

Hint: Proving sides of two triangles equal can be done by proving these triangles are congruent. We can use various congruence theorems according to the information provided. Here as we have the information about sides and angles from the fact that there is a square and an equilateral triangle, use SAS(Side Angle Side) Congruence theorem – Two triangles are congruent when two sides and corresponding interior angles are equal to that of another triangle.

Complete step-by-step answer:
Step 1: As a portion of the given figure, PQRS is a square,
Implies all sides are equal: PQ=QR=RS=SP.
 And all angles are right angles: $\angle PQR = \angle QRS = \angle RSP = \angle SPQ = {90^0}$
Step 2: As the other portion $\vartriangle SRT$ is an equilateral triangle,
All sides are equal: SR=RT=TS.
All angles = ${60^0}$ implies $\angle SRT = \angle RTS = \angle TSR$ = ${60^0}$
Step 3: From equivalence of sides of square and triangle, PQ=QR=SP=SR=RT=TS
As we need to prove PT = QT consider the triangles containing these sides $\vartriangle TSP$ and $\vartriangle TRQ$ ,
$
  \angle TSP = \angle TSR + \angle RSP \\
   = {60^0} + {90^0} \\
   = {150^0} \\
 $
$
  \angle TRQ = \angle TRS + \angle SRQ \\
   = {60^0} + {90^0} \\
   = {150^0} \\
 $
Thus $\angle TSP = \angle TRQ = {150^0}$ which shows corresponding angles of $\vartriangle TSP$ and $\vartriangle TRQ$ are equal.
And also TS=TR , SP=RQ which are the two side equalities required to prove the congruence
Thus by Side Angle Side congruence theorem : when two sides and an angle of two triangles are equal, those triangles are congruent.
Implies PT=QT

Note: Similarly there are other congruence theorems of triangles which can be applied : SSS(Side Side Side ) congruence, ASA(Angle Side Angle) congruence, AAS(Angle Angle Side) congruence theorem. Choose a proper congruence theorem according to the information provided.