Question

In fig. $ P $ is a point in the interior of a parallelogram ABCD. Show that
(i) $ ar(APB) + ar(PCD) = \dfrac{1}{2}ar(ABCD) $
(ii) $ ar(APD) + ar(PBC) = ar(APB) + ar(PCD) $

Answer 1

Hint: First of all it is given that the quadrilateral shown in the figure is a parallelogram. Further we will take a triangle and a parallelogram; they have the same base between the parallel lines. Then by using , area of triangle $ = \dfrac{1}{2}area $ of parallelogram.

Complete step-by-step answer:

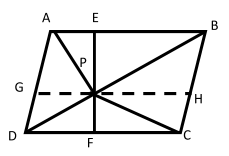
: $ ABCD $ is a parallelogram and $ P $ is the interior point
To prove (i) ar\[(APB) + ar(PCD) = \dfrac{1}{2}ar(ABCD)\]
(ii) $ ar(APD) + ar(PBC) = ar(APB) + ar(PCD) $
Construction: Draw a line $ EF $ through P and parallel to $ BC $ and $ GH $ through point $ P $ and parallel to AB
Proof: Since ABCD is a parallelogram
(i) So, $ AB||CD $ (opposite sides of a parallelogram are parallel)
 And $ AD||BC $
Now, $ GH||AB $ and $ AB||CD $
Then $ AB||GH||CD $
\[\therefore ABHG\] is a parallelogram because $ AB||GH $ and $ GHCD $ is also a parallelogram, because $ GH||CD $
Now, in parallelogram $ ABHG $ and triangle $ APB $ have same base $ AB $ and between the same parallel line $ AB\,\,and\,\,GH $
 $ \therefore $ Area $ (\Delta APB) = \dfrac{1}{2}area(ABHG) $ ….(i)
As we know that area of a triangle is half of parallelogram if they have the same base and between parallel lines
In parallelogram $ GHCD $ and a triangle $ DPC $ have the same base $ CD $ and between the same parallel line $ CD\,\,and\,\,GH $ .
 $ \therefore ar(\Delta DPC) = \dfrac{1}{2}ar(GHCD) $ ……(ii)
As we know that area of a triangle is half of the parallelogram if they have the same base and between the parallel lines
Adding equation (i) and (ii) we will get
 $ ar(\Delta APB) + ar(\Delta dpc) = \dfrac{1}{2}ar(ABHG) + \dfrac{1}{2}ar(GHCD) $
 $ ar(\Delta APB) + ar(\Delta DPC) = \dfrac{1}{2}\left[ {ar(ABHG) + ar(GHCD)} \right] $
 $ ar(\Delta APB) + ar(\Delta DPC) $ $ = \dfrac{1}{2}ar(ABCD) $ …..(iii)
Hence prove (i)
(iii) Now $ EF||BC $ (by construction)
And $ AD||BC $ (opposite sides of parallelogram are parallel)
So, $ EF||BC||AD $
 $ \therefore AEFD\,\,and\,\,EBCD $ are parallelogram as $ EF||AD\,\,and\,\,EF||AC $
Now, triangle $ APD $ and a parallelogram $ AE $ $ FD $ have same base $ AD $ and between parallel lines are $ AD $ and $ EF $ ….(iv)
As we know that area of the triangle is half of the parallelogram if they have the same base between the parallel lines.
Triangle $ PBC $ and parallelogram $ EFCB $ have same base $ BC $ and between parallel lines $ EF\,\,and\,\,BC $
 $ ar(\Delta PBC) = \dfrac{1}{2}AR(EFCB) $ ……(v)
Adding equation (iv) and (v), we have
 $ ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(AEFD) + \dfrac{1}{2}ar(EFCB) $
 $ ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(AEFD) + ar(EFCB) $
 $ ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(ABCD) $ …..(vi)
From equation (iii) and (vi), we will get
\[ar(\Delta APB) + ar(\Delta DPC) = ar(\Delta APB) + ar(\Delta PBC)\]

Note: Students keep in mind that if a triangle and parallelogram have the same base and between same parallel lines then the area of a triangle is equal to half of the parallelogram.