Question

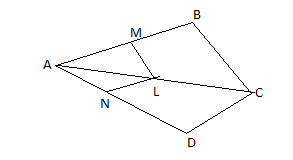
In Fig, if $LM\parallel CB$ and $LN\parallel CD$, prove $\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AD}}$

Answer 1

Hint: Firstly, we need to consider the diagram that is mentioned above. Then by applying proportionality theorem we can prove that $\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AD}}$.

Complete step-by-step answer:
It is given that $LM\parallel CB$ and $LN\parallel CD$
From the diagram we see that in $\Delta ABC$,
 It is given that $LM\parallel CB$
∴ By applying proportionality theorem we get
$\dfrac{{AM}}{{MB}} = \dfrac{{AL}}{{LC}}....\left( 1 \right)$
In a similar way, in $\Delta ADC$ we get-
 It is also mentioned in the question that $LN\parallel CD$
Again, by applying proportionality theorem we get-
$\dfrac{{AN}}{{ND}} = \dfrac{{AL}}{{LC}}....\left( 2 \right)$
From equations $\left( 1 \right){\text{and }}\left( 2 \right)$ it is clear that since both $\dfrac{{AM}}{{MB}}$and $\dfrac{{AN}}{{ND}}$ equals to $\dfrac{{AL}}{{LC}}$
 Therefore, $\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{ND}}$
 Now, by applying the principle of invertendo we get-
$\dfrac{{MB}}{{AM}} = \dfrac{{ND}}{{AN}}$
Now by adding $1$on both the sides we get,
$\dfrac{{MB}}{{AM}} + 1 = $$\dfrac{{ND}}{{AN}} + 1$
Taking LCM on both sides we get,
$\dfrac{{MB + AM}}{{AM}} = \dfrac{{ND + AN}}{{AN}}$
From the given diagram shows that ${\text{MB + AM = AB}}$and ${\text{ND + AN = AD}}$we get,
$\dfrac{{AB}}{{AM}} = \dfrac{{AD}}{{AN}}$
Again, by applying the principle of invertendo we get-
$\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AD}}$

Hence, it is proved that $\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AD}}$

Note: According to proportionality theorem, when a line is drawn parallel to any of the sides of the triangle intersecting the remaining two sides of the triangle, then it divides the two sides in the same ratio.
Invertendo means inverse for example if two ratios suppose, $\dfrac{a}{b} = \dfrac{c}{d}$ then $\dfrac{b}{a} = \dfrac{d}{c}$
Greek mathematicians have introduced the famous basic proportionality theorem which is known as Thales theorem. According to him, the ratio of any two corresponding sides of two equilateral triangles must be the same.
Two triangles will be similar only if the corresponding sides of the two triangles are equal or corresponding angles of the two triangles are equal.
It is to be kept in mind that similar triangles will have the same shape but that does not mean similar triangles will have the same size always.