Question

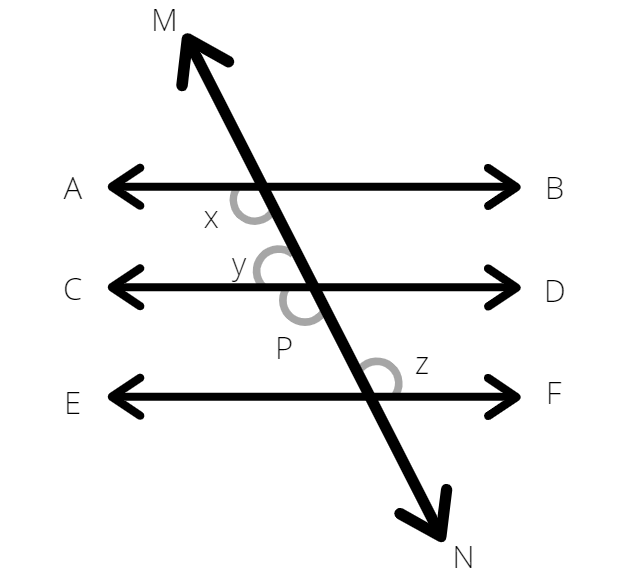
In fig if AB$||$CD, CD$||$EF and $y:z = 3:7$ find $x$

Answer 1

Hint: This sum involves application of properties of lines. The student has to make use of the properties like Corresponding Angles, Alternate Angles and sum of interior angles on the same side of the transversal is ${180^ \circ }$. This sum is extremely to solve and should involve no margin of error.

Complete answer:
From the figure we can see that it is given $\dfrac{y}{z} = \dfrac{3}{7}$
$\therefore y = \dfrac{3}{7}z$
Let $\angle CON = P$
Given CD$||$EF,
We can Say that $P = z$, Since they are Alternate Interior Angles
Also from the figure we can say
$\Rightarrow$ $y + P = {180^ \circ }$ Using the property i.e. sum of interior angles on same side of transversal is ${180^ \circ }$.
Now we can say that
$\Rightarrow$$y + z = {180^ \circ }$,
Also we know,
$\therefore y = \dfrac{3}{7}z$,
$\Rightarrow$$\dfrac{3}{7}z + z = {180^ \circ }$
$\therefore z = \dfrac{7}{{10}} \times {180^ \circ } = {126^ \circ }$
Putting $z = {126^ \circ }$,we get the value of $y$
$\therefore y = \dfrac{3}{7} \times 126 = {54^ \circ }$.
Also we can say that
$\Rightarrow$ $x + y = {180^ \circ }$,
Using the property i.e. sum of interior angles on the same side of transversal is ${180^ \circ }$.
$\therefore x = {180^ \circ } - {54^ \circ }$

$\therefore x = {126^ \circ }$

Note: It is important to note that the sums on geometry can be solved only if the student is well versed with the properties of the figures. Also sometimes the corollary of the properties can be used to solve the problems, so it is important to thoroughly study the properties.