Question

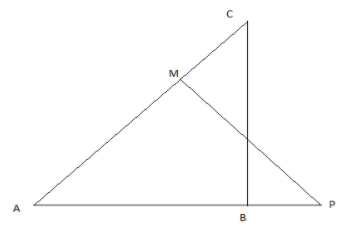
In fig., \[\Delta ABC\] and \[\Delta AMP\] are two right-angle triangles, right angled at \[B\] and \[M\] respectively. Prove that:
(i). \[\Delta ABC \sim \Delta AMP\]
(ii). \[\dfrac{{CA}}{{PA}} = \dfrac{{BC}}{{MP}}\]
               

Answer 1

Hint: We know that; for any two right-angle triangles, if one of the other two angles is equal then the third angle is also equal to each other. This condition is known as A-A-A similarity condition. Then, we can say that the triangles are similar.
By using the condition of similarity, we can prove the given triangles are similar.
Again, we know that, if two triangles are similar to each other, then the ratio of their corresponding sides is proportional. Using this condition, we can prove the second problem.

Complete step-by-step answer:
It is given that; \[\Delta ABC\] and \[\Delta AMP\] are two right-angle triangles, right angled at \[B\] and \[M\] respectively. So, \[\angle ABC = {90^ \circ }\] and \[\angle AMP = {90^ \circ }\]
We have to show that,
(i). \[\Delta ABC \sim \Delta AMP\]
(ii). \[\dfrac{{CA}}{{PA}} = \dfrac{{BC}}{{MP}}\]
To prove: \[\Delta ABC \sim \Delta AMP\]
Here, \[\angle ABC = \angle AMP\] (as both are \[{90^ \circ }\]).
\[\angle CAB = \angle MAP\] as they are common angles.
So, by A-A similarity \[\Delta ABC \sim \Delta AMP\].
Again, to prove \[\dfrac{{CA}}{{PA}} = \dfrac{{BC}}{{MP}}\]
Since, \[\Delta ABC\] and \[\Delta AMP\] are similar triangles, the ratio of their corresponding sides is proportional.
So, we have,
\[\dfrac{{CA}}{{PA}} = \dfrac{{BC}}{{MP}} = \dfrac{{AB}}{{AM}}\]
From the relation we get,
\[\dfrac{{CA}}{{PA}} = \dfrac{{BC}}{{MP}}\]

Note: If the three angles of any triangle are equal to the respective angles of another triangle, then the triangle is called a similar triangle.
For any two right-angle triangles, if one of the other two angles is equal then the third angle is also equal to each other.
If two triangles are similar to each other, then the ratio of their corresponding sides is proportional.