Question

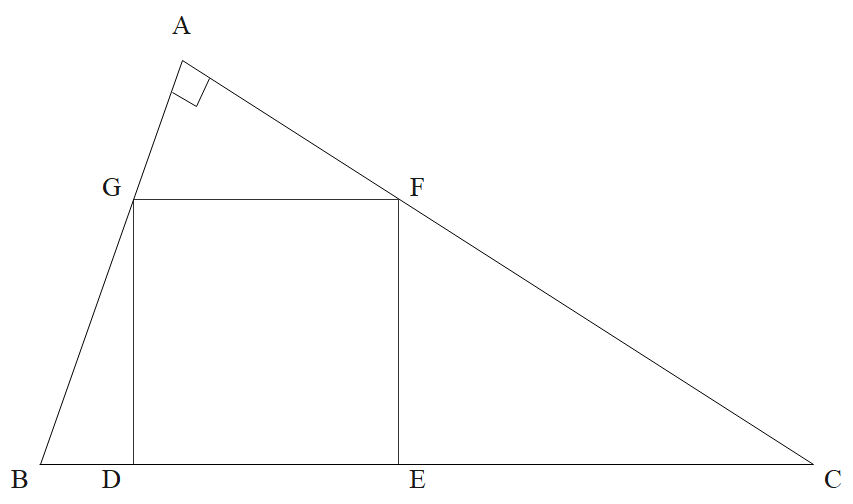
In Fig., DEFG is a square in a triangle ABC right angled at A. Prove that
i) $\Delta \mathrm{AGF} \sim \Delta \mathrm{DBG}$
ii) $\Delta \mathrm{AGF} \sim \Delta \mathrm{EFC}$

Answer 1

Hint: The height of a triangle is the distance from the base to the highest point, and in a right triangle that will be found by the side adjoining the base at a right angle. The Pythagorean theorem states that: In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

Complete step-by-step answer:
Right triangles are triangles in which one of the interior angles is 90 degrees, a right angle. since the three interior angles of a triangle add up to 180 degrees, in a right triangle, since one angle is always 90 degrees, the other two must always add up to 90 degrees (they are complementary). In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle. We use special words to describe the sides of right triangles.
DEFG is a square,
$\Rightarrow \mathrm{GF} \| \mathrm{DE}$
$\therefore \mathrm{GF} \| \mathrm{BC}$
Now, In $\Delta \mathrm{AGF}$ and $\Delta \mathrm{DBG}$
$\angle \mathrm{AGF}=\angle \mathrm{DBG} \quad[\because \mathrm{GF} \| \mathrm{BC}]$
and, $\angle \mathrm{BDG}=\angle \mathrm{GAF}=90^{\circ}$
$\therefore \Delta \mathrm{AGF} \sim \Delta \mathrm{DBG} \quad[\mathrm{AA}]$
Now, In $\Delta \mathrm{AGF}$ and $\Delta \mathrm{EFC}$
$\angle \mathrm{AFG}=\angle \mathrm{ECF} \quad[\because \mathrm{GF} \| \mathrm{BC}]$
and, $\angle \mathrm{FAG}=\angle \mathrm{CEF}=90^{\circ}$
$\therefore \Delta \mathrm{AGF} \sim \Delta \mathrm{EFC} \quad[\mathrm{AA}]$

Note: A triangle that has three acute angles is called an acute triangle. A triangle that has one right angle is called a right triangle. A triangle that has one obtuse angle is called an obtuse triangle. Since a triangle's angles must sum to $180^{\circ}$ in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle. Acute and obtuse triangles are the two different types of oblique triangles - triangles that are not right triangles because they have no $90^{\circ}$ angle.