Question

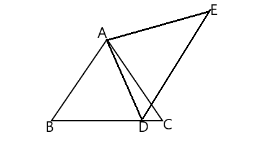
In fig. $ AC = AE,AB = AD $ and $ \angle BAD = \angle EAC. $ Show that $ BC = DE. $

Answer 1

Hint: As we can see that there are two triangles in the questions. We can use the congruence criteria to prove that $ BC = DE $ . Congruent means exactly the same replica of one another i.e. equal in all respects or figures. We will prove that both the triangles are congruent and then we can get the required solution. We know that two triangles are said to be congruent if all of its sides and angles are equal. WE can show that two triangles are congruent by the congruence rules.

Complete step by step solution:
As per the given figure we have been given that, $ AC = AE,AB = AD $ and $ \angle BAD = \angle EAC. $ Here we have $ \angle BAD = \angle EAC. $ ,
we will add $ \angle DAC $ on both the sides and we have:
 $ \angle BAD + \angle DAC = \angle EAC + \angle DAC $ ,
and it gives, $ \angle BAC = \angle DAE $ .
Now in $ \Delta BAC $ and $ \Delta DAE $ , $ AB = AD $ (given)
 $ \angle BAC = \angle DAE $ (as we proved above) and $ AC = AE $ . So we can say that by $ SAS $ congruence $ \Delta BAC \cong \Delta DAE $ .
Hence $ BC = DE $ By the corresponding parts of the congruent triangles i.e. By CPCT.

Note: We should note that if two sides and the angle included between the two sides of one triangle are equal to the corresponding sides and the included angle of the another triangle then the two triangles are congruent to each other. We should know all the congruence criteria and their methods before solving this kind of question. And the congruence of two triangles is represented by the symbol $ \cong $ .