Question

In Fig. a massive rod AB is held in a horizontal position by two massless strings. If the string at B breaks and if the horizontal acceleration of centre of mass, vertical acceleration and angular acceleration of rod about the centre of mass are  ${a_x}$​, ${a_y}$​ and $\alpha $  respectively, then

A) $2\sqrt 3 ay$ =$\sqrt 3 \alpha l$ +2${a_x}$​
B) $\sqrt 3 {a_y}$ =$\sqrt 3 \alpha l$ +${a_x}$
C) ${a_y}$​=$\sqrt 3 \alpha l$ +${2_\alpha }x$
D) $2{a_y}$ =$\alpha l$ +$2\sqrt 3 {a_x}$

Answer 1

Hint: The question is a bit tricky and can easily be solved by making a diagram according to the components of sin and cos. For some help below diagram is provided. The component $T\cos {30^0}$ provides horizontal acceleration $ax$ to rod and the same way the component $T\sin {30^o}$ provides torque too. Then by equating it with angular acceleration with center of mass m we will find our solution.

Step by step solution:
Step 1:
Assuming tension in string A be T and length of rod AB be L, with mass m.
Here c is the center of mass. For more clarity let us consider the diagram below:

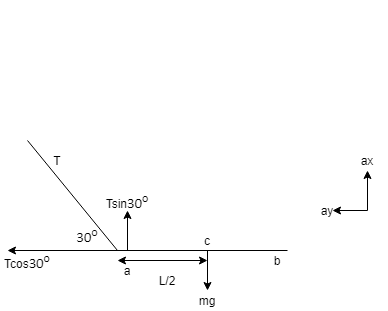
Step 2:
The component $T\cos {30^0}$ provides horizontal acceleration $ax$ to rod and $ax$=$\dfrac{{T\cos {{30}^0}}}{M}$
 The component $T\sin {30^o}$ provides torque, torque= $T\sin {30^o}$×$\dfrac{L}{2}$
This is equal to $\dfrac{{TL}}{4}$ …. (1)
And in vertical using Newton’s law May= $T\sin {30^o}$−Mg $ \Rightarrow $ ay=$\left( {\dfrac{T}{{2M}} - g} \right)$ ………. (2)
The torque provides necessary angular acceleration, torque=$I\alpha $
Where I about center of mass C is $\dfrac{{M{L^2}}}{{12}}$….. (3)
Equating (1) and (3) together and putting the value of torque $\dfrac{{TL}}{4}$= $\dfrac{{M{L^2}}}{{12}}$
This implies $\dfrac{T}{M}$ =$\dfrac{{\alpha L}}{3}$……. (4)
Hence, from equation (1), (2) and (4) we get $ax$=$\dfrac{{\alpha L\cos {{30}_o}}}{3}$ which is equal to $\dfrac{{\alpha L}}{{2\sqrt 3 }}$
And $ay$=$\dfrac{{\alpha L}}{6} - g$
Thus we get 2ay=2$\sqrt 3 $ax +$\alpha L$

Hence option D is correct.

Note:Point of mistake: The whole solution depends upon the diagram provided in the question and the other one which is made on the basis of the components of the vector. Without this diagram the question is tricky to solve so make it error free. Second thing is the numerical part, assign the equation number before proceeding so as to use and equate where ever necessary.