Question

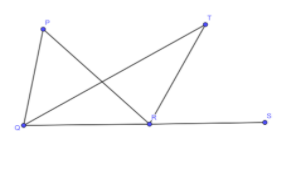
In fig 6.44 , the side QR of triangle PQR is produced to a point S. If the bisectors of angle PQR and angle PRS meet at point T, then prove that $\angle QTR = \dfrac{1}{2}\angle QPR$

Answer 1

Hint: Use exterior angle theorem on separating the two triangles and prove the required statement.
 With the given condition of TQ bisecting $\angle PQR$, we get a new statement or condition and from observing the diagram, we observe that TR is bisecting $\angle PRS$. So, here also we get a new condition statement. Then we separately consider the two triangles which are combined in the diagram. Then apply the external angle theorem on those two triangles, which gives another two-condition statement. Now using these statements, we substitute the bisector condition statements accordingly into the new statements, then solving the equation formed proves the problem statement given in the question.

Complete step by step answer:
Given that
TQ is the bisector of $\angle PQR$,
So, it implies that
Condition (1)
$\angle PQT = \angle TQR = \dfrac{1}{2}\angle PQR$
Also, from the diagram, we can say that
TR is the bisector of $\angle PRS$. So, it implies
Condition (2)
$\angle PRT = \angle TRS = \dfrac{1}{2}\angle PRS$
Now, we consider the two triangles separately $\vartriangle PQR$ and $\vartriangle TQR$

So, in $\vartriangle PQR$,
\[
  \dfrac{1}{2}\left( {\angle QPR + \angle PQR} \right) = \dfrac{1}{2}\angle PQR + \angle QTR \\
  \dfrac{1}{2}\angle QPR + \dfrac{1}{2}\angle PQR - \dfrac{1}{2}\angle PQR = \angle QTR \\
  \dfrac{1}{2}\angle QPR = \angle QTR \\
\] is the external angle
By using external angle theorem, which is “External angle is the sum of two interior opposite angles”.
With this, we get
Condition (3)
$\angle PRS = \angle QPR + \angle PQR$
Now, coming to the other triangle $\vartriangle TQR$
\[\angle TRS\] is the external angle, so by the external angle theorem, which is “External angle is the sum of two interior opposite angles”. We get
Condition (4)
\[\angle TRS = \angle TQR + \angle QTR\].
We substitute the condition 1 and condition 2 to condition 4. We get
\[
  \dfrac{1}{2}\angle PRS = \dfrac{1}{2}\angle PQR + \angle QTR \\
  \dfrac{1}{2}\angle PRS = \dfrac{1}{2}\angle PQR + \angle QTR \\
\]
Now we use the condition 3 for substitution
\[
  \dfrac{1}{2}\left( {\angle QPR + \angle PQR} \right) = \dfrac{1}{2}\angle PQR + \angle QTR \\
  \dfrac{1}{2}\angle QPR + \dfrac{1}{2}\angle PQR - \dfrac{1}{2}\angle PQR = \angle QTR \\
  \dfrac{1}{2}\angle QPR = \angle QTR \\
\]
Hence, we have successfully proved what is required.

Note: The bisector of a triangle divides the angle in two equal halves through which it passes and the external angle theorem is only applicable for interior and most importantly opposite angle and not adjacent angles.