Question

In fig 4 triangle ABC is a right triangle with AB = 6cm, AC =8cm and $ \angle A={{90}^{\circ }} $ . A circle is inscribed inside the triangle. Find the radius ‘r’.

Answer 1

Hint: Given a triangle is a right triangle and its two sides are given so by using Pythagorean theorems, we can find the third side. We know that the inscribed circle radius is perpendicular on a point where the circle touches the sides of the triangle (because the triangle's side works as a tangent for the circle). So we will split the triangle into 3 small triangles and then apply the area of the triangles formula to find ‘r’.

Complete step-by-step answer:
In triangle ABC,
AB= 6cm
AC= 8cm
BC=?
Pythagorean theorems states,
 $ hypotenuse{{e}^{2}}=bas{{e}^{2}}+heigh{{t}^{2}} $
Using this theorem in above triangle,
 $ B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}} $
Substituting AC=8 and AB=6
 $ \begin{align}
  & B{{C}^{2}}={{8}^{2}}+{{6}^{2}} \\
 & B{{C}^{2}}=64+36 \\
 & BC=10 \\
\end{align} $
Let O be the center of the circle. Draw perpendicular lines from O to each side. Now each side will work as a tangent of the circle . That's why the radius is perpendicular to the point where the circle touches the sides of the triangle.
And we also know that area of a circle = $ \dfrac{1}{2}\times base\times height $
 

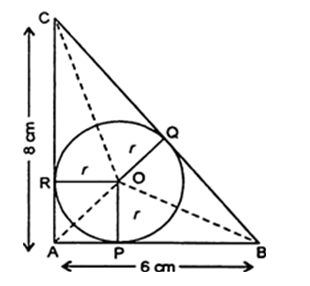
  Now we have
Area of ABC= Area of AOC + Area of AOB + Area of BOC
 $ \dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times OR\times AC+\dfrac{1}{2}\times OP\times AB+\dfrac{1}{2}\times OQ\times BC $
 $ \dfrac{1}{2}\times 8\times 6=\dfrac{1}{2}\times r\times 8+\dfrac{1}{2}\times r\times 6+\dfrac{1}{2}\times r\times 10 $
Multiply by 2 to both sides.
 $ 48=r(8+6+10) $
 $ r=\dfrac{48}{24}=2 $

Note:OP, OR and OQ are perpendicular on AB, AC and BC that’s why we can use r as a height in triangle AOB, BOC and AOC. In a right triangle base and height is interchangeable. By above solution we can also conclude that,
Area of a triangle = ½ (radius of inscribed circle in that triangle) (perimeter of triangle)