Question

In $\Delta PQR$ , right angled at Q, $PR+QR=25cm$ and $PQ=5cm$ . Determine the value of$\sin P,\cos P,\tan P$.

Answer 1

Hint: First of all find all the sides of the triangle. As PQ is given, PR + QR are also given so using Pythagoras theorem we can find the values of PR and QR. Now, using trigonometric ratios we can find $\sin P,\cos P,\tan P$ .

Complete step-by-step answer:
The below figure describes a$\Delta PQR$right angled at Q having 3 sides with $PQ=5cm$ .

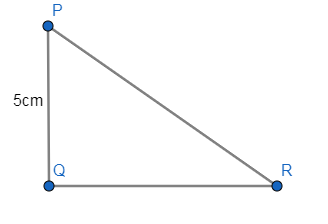
 In the question, it is given that:
$PQ=5cm$
$PR+QR=25cm$ ………Eq. (2)
As PQR is a right triangle, so we can use Pythagoras theorem which states that:
$P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}$ PR2 = PQ2 + QR2
From eq. (2) we can write $PR=25-QR$ and then substituting in the above equation will give: $\begin{align}
  & {{\left( 25-QR \right)}^{2}}=P{{Q}^{2}}+Q{{R}^{2}} \\
 & \Rightarrow 625+Q{{R}^{2}}-50QR={{\left( 5 \right)}^{2}}+Q{{R}^{2}} \\
 & \Rightarrow 625-50QR=25 \\
 & \Rightarrow 600=50QR \\
 & \Rightarrow QR=12 \\
\end{align}$
From the above calculation we have got $QR=12cm$ .
Now, substituting this value of QR in eq. (1) we get,
$\begin{align}
  & PR+QR=25cm \\
 & PR=25-12 \\
 & PR=13 \\
\end{align}$
From the above calculation we have got $PR=13cm$ .
Now, we know all the sides of the triangle.
PQ = 5cm, PR = 13cm and QR = 12cm
We are going to find the values of $\sin P,\cos P,\tan P$ .
We know that $\sin P=\dfrac{P}{H}$ where “P” stands for the perpendicular of the triangle with respect to angle P and “H” stands for the hypotenuse of the triangle with respect to angle P.
So, in the given triangle for $\sin P$ the perpendicular is QR and the hypotenuse is PR.
$\begin{align}
  & \sin P=\dfrac{QR}{PR} \\
 & \Rightarrow \sin P=\dfrac{12}{13} \\
\end{align}$
We know that $\cos P=\dfrac{B}{H}$ where “B” stands for the base of the triangle with respect to angle P and “H” stands for the hypotenuse of the triangle with respect to angle P.
So, in the given triangle for $\cos P$ the base (B) is QR and the hypotenuse (H) is PR.
$\begin{align}
  & \cos P=\dfrac{PQ}{PR} \\
 & \Rightarrow \cos P=\dfrac{5}{13} \\
\end{align}$
We know that $\tan P=\dfrac{P}{B}$ where “B” stands for the base of the triangle with respect to angle P and “P” stands for the perpendicular of the triangle with respect to angle P
So, in the given triangle for $\tan P$ the base (B) is QR and the perpendicular (P) is QR.

$\begin{align}
  & \tan P=\dfrac{QR}{PQ} \\
 & \Rightarrow \tan P=\dfrac{12}{5} \\
\end{align}$
From the above calculations, the values of $\sin P,\cos P,\tan P$ are as follows:
$\sin P=\dfrac{12}{13},\cos P=\dfrac{5}{13}\And \tan P=\dfrac{12}{5}$

Note: You can verify that the values of $\sin P,\cos P,\tan P$ are correct or not.
The values of $\sin P\text{ and }\cos P$ is:
$\sin P=\dfrac{12}{13}\And \cos P=\dfrac{5}{13}$
As you can see both the cosine and sine of P are less than 1 and we already know that the value of sine and cosine cannot exceed 1 so the answer that we are getting is correct.
The value of $\tan P$ is:
$\tan P=\dfrac{12}{5}$
The value of tan P from the above equation is greater than 1 and we know that tan of an angle can take any values from -∞ to ∞ so the answer that we are getting is correct.