Question

In $\Delta PQR$, right angled at Q, PQ = 3cm and PR = 6cm. Determine $\angle QPR \And \angle PRQ$.

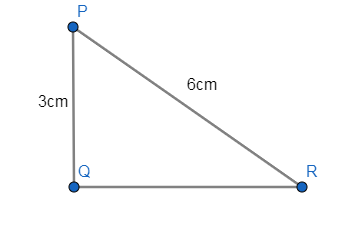
Answer 1

Hint: The given question contains a right angled $\Delta PQR$; two sides PQ and PR so from trigonometric ratios we can find the values of $\angle QPR\And \angle PRQ$. Let us assume $\angle PRQ=\theta $ and $\angle QPR=\alpha $ so $\sin \theta =\dfrac{PQ}{PR}$and from this ratio we can find $\angle PRQ$. We know that $\cos \alpha =\dfrac{PQ}{PR}$ so from this ratio we can find $\angle QPR$.

Complete step-by-step answer:

The below figure shows a $\Delta PQR$ right angled at Q with two sides PQ and PR are given as 3cm and 6cm respectively.

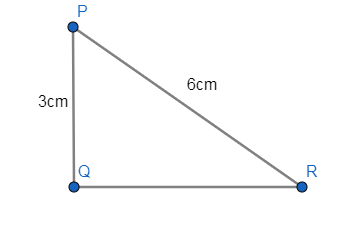
Let us assume that $\angle PRQ=\theta $ & $\angle QPR=\alpha $.

From the trigonometric ratios we know that,

$\sin \theta =\dfrac{P}{H}$

In the above equation, P stands for perpendicular or the side just opposite to angle θ and H stands for hypotenuse of the right $\Delta PQR$.

$\sin \theta =\dfrac{PQ}{PR}$

It is given that PQ = 3cm and PR = 6cm. Substituting these values in the above equation we get,

$\begin{align}

  & \sin \theta =\dfrac{3}{6} \\

 & \Rightarrow \sin \theta =\dfrac{1}{2} \\

\end{align}$

We know that when $\sin \theta =\dfrac{1}{2}$ then the value of θ is equal to 30°.

As we have assumed that $\angle PRQ=\theta $ so $\angle PRQ={{30}^{\circ }}$.

From the trigonometric ratios we know that,

$\cos \alpha =\dfrac{B}{H}$

In the above equation, B stands for the base of the triangle with respect to angle α and H stands for hypotenuse of the right $\Delta PQR$.

$\begin{align}

  & \cos \alpha =\dfrac{PQ}{\operatorname{P}R} \\

 & \Rightarrow \cos \alpha =\dfrac{3}{6} \\

 & \Rightarrow \cos \alpha =\dfrac{1}{2} \\

\end{align}$

When $\cos \alpha =\dfrac{1}{2}$ then the value of angle α is 60°.

As we have assumed that $\angle QPR=\alpha $ so $\angle QPR={{60}^{\circ }}$.

Hence, we have calculated the value of $\angle PRQ={{30}^{\circ }}\And \angle QPR={{60}^{\circ }}$.

Note: You can check whether the angles that you are getting are correct or not. As angle Q is already given as 90°and we have calculated the values of $\angle QPR\And \angle PRQ$. And the sum of all the angles of a triangle is 180°.

$\angle PQR+\angle QPR+\angle PRQ={{180}^{\circ }}$

Adding L.H.S of the above equation will give:

$\begin{align}

  & {{90}^{\circ }}+{{60}^{\circ }}+{{30}^{\circ }} \\

 & ={{180}^{\circ }} \\

\end{align}$

From the above calculation L.H.S = R.H.S so the angles that we have calculated are correct.